题目内容
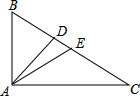 如图,在△ABC中,∠BAC=90°,AB=3cm,AC=4cm,AD是高线,AE是中线.
如图,在△ABC中,∠BAC=90°,AB=3cm,AC=4cm,AD是高线,AE是中线.(1)以点A为圆心,3cm为半径作⊙A,则点B,D,E,C与⊙A的位置关系怎样?
(2)若以点A为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围.
考点:点与圆的位置关系
专题:
分析:(1)先利用勾股定理计算出BC=5cm,再利用面积法求出AD=
cm,根据直角三角形斜边上的中线性质得AE=2.5cm,则AB=r,AD<r,AE<r,AC>r,
然后根据点与圆的位置关系进行判断;
(2)根据题意点D只能在圆内,点C只能在圆外,所)⊙A的半径r的取值范围为
<r<4.
| 12 |
| 5 |
然后根据点与圆的位置关系进行判断;
(2)根据题意点D只能在圆内,点C只能在圆外,所)⊙A的半径r的取值范围为
| 12 |
| 5 |
解答:解:(1)∵∠BAC=90°,AB=3cm,AC=4cm,
∴BC=
=5cm,
∵
AD•BC=
AB•AC,
∴AD=
cm,
∵AE是中线,
∴AE=
BC=2.5cm,
∵r=3cm,
∴AB=r,AD<r,AE<r,AC>r,
∴点B在⊙A上,点D、点E在⊙A内,点C在⊙A外;
(2)⊙A的半径r的取值范围为
<r<4.
∴BC=
| AB2+AC2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| 12 |
| 5 |
∵AE是中线,
∴AE=
| 1 |
| 2 |
∵r=3cm,
∴AB=r,AD<r,AE<r,AC>r,
∴点B在⊙A上,点D、点E在⊙A内,点C在⊙A外;
(2)⊙A的半径r的取值范围为
| 12 |
| 5 |
点评:本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外?d>r;点P在圆上?d=r;点P在圆内?d<r.

练习册系列答案
相关题目
 如图,一个有弹性的小球从点A下落到地面,弹起到点B后,再次落到地面又弹起到点C,已知弹起的高度是之前落下高度的80%.
如图,一个有弹性的小球从点A下落到地面,弹起到点B后,再次落到地面又弹起到点C,已知弹起的高度是之前落下高度的80%.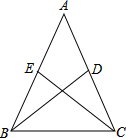 已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.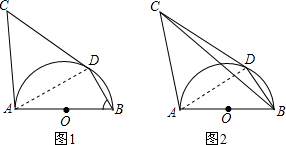 已知AC、CD分别切⊙O于A、D两点,连接BD.
已知AC、CD分别切⊙O于A、D两点,连接BD.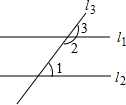 用反证法证明:两直线平行,同旁内角互补(填空).
用反证法证明:两直线平行,同旁内角互补(填空).