题目内容
6.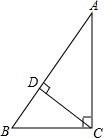 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,则cot∠BCD的值为( )
如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,则cot∠BCD的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{12}{5}$ | D. | $\frac{12}{13}$ |
分析 根据在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,可以得到∠A和∠BCD的关系,由∠A的三角函数值可以得到∠BCD的三角函数值,从而可以解答本题.
解答 解:∵在Rt△ABC中,∠C=90°,
∴∠B+∠A=90°,
∵CD⊥AB于点D,
∴∠CDB=90°,
∴∠B+∠BCD=90°,
∴∠A=∠BCD,
∵在Rt△ABC中,∠C=90°,AC=12,BC=5,
∴cot∠A=$\frac{AC}{BC}=\frac{12}{5}$,
∴cot∠BCD=$\frac{12}{5}$.
故选C.
点评 本题考查解直角三角形,解题的关键是找出各个角之间的关系,根据等角的三角函数值相等,运用数学转化的思想进行解答问题.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 没有最小的正数 | B. | -a表示负数 | ||
| C. | 符号相反两个数互为相反数 | D. | 一个数的绝对值一定是正数 |
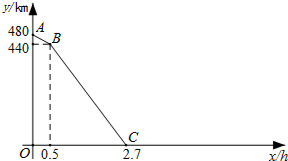 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象. 如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一个动点(不与A、B重合),作EF⊥AB交边BC于点F,联结AF、EC交于点G.
如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一个动点(不与A、B重合),作EF⊥AB交边BC于点F,联结AF、EC交于点G.