题目内容
已知,抛物线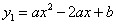 经过A(-1,0),C(2,
经过A(-1,0),C(2,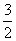 )两点,
)两点,
与x轴交于另一点B.
(1)求此抛物线的解析式;
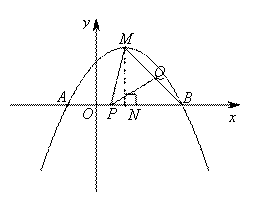
(2)若抛物线的顶点为M,点P为线段OB上一动点 (不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ= ,求y2与x的函数关系式,
,求y2与x的函数关系式,
并直接写出自变量x的取值范围.
 |
解:(1) ∵拋物线y1=ax2-2ax+b经过A(-1,0),C(0,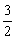 )两点,
)两点,
∴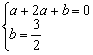 ,∴
,∴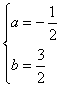 ,∴拋物线的解析式为y1= -
,∴拋物线的解析式为y1= -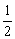 x2+x+
x2+x+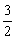
(2)解法一:过点M作MN⊥AB交AB于点N,连接AM
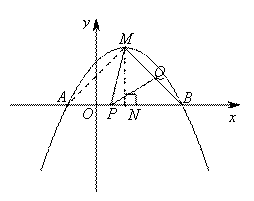 由y1= -
由y1= -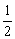 x2+x+
x2+x+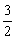 可知顶点M(1,2) ,A(-1,0),B(3,0),N(1,0)
可知顶点M(1,2) ,A(-1,0),B(3,0),N(1,0)
∴AB=4,MN=BN=AN=2,AM=MB=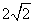 .
.
∴△AMN和△BMN为等腰直角三角形.
∵∠MPA+∠QPB=∠MPA +∠PMA=135°
∴∠QPB=∠PMA
又∵∠QBP=∠PAM=45°∴△QPB∽△PMA
∴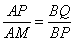 将AM=
将AM=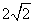 ,AP=x+1,BP=3-x,BQ=
,AP=x+1,BP=3-x,BQ= 代入,
代入,
 可得
可得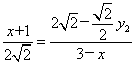 ,即
,即 .
.
∵点P为线段OB上一动点 (不与点B重合)∴0£x<3
则y2与x的函数关系式为y2=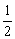 x2-x+
x2-x+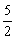 (0£x<3)
(0£x<3)
解法二:
过点M作MN⊥AB交AB于点N.
由y1= -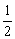 x2+x+
x2+x+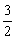 易得M(1,2),N(1,0),A(-1,0),B(3,0),
易得M(1,2),N(1,0),A(-1,0),B(3,0),
∴AB=4,MN=BN=2,MB=2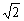 ,ÐMBN=45°
,ÐMBN=45°
根据勾股定理有BM 2-BN 2=PM 2-PN 2. ∴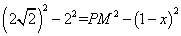 …①,
…①,
又ÐMPQ=45°=ÐMBP,∴△MPQ∽△MBP,∴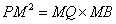 =
=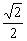 y2´2
y2´2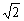
由j、k得y2=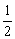 x2-x+
x2-x+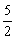 .
.
∵0£x<3,∴y2与x的函数关系式为y2=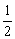 x2-x+
x2-x+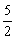 (0£x<3)
(0£x<3)

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 )中的计算结果的规律填空:
)中的计算结果的规律填空: ,
, 的取值范围是 .
的取值范围是 . 
 .
.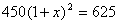 B.
B.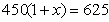
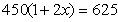 D.
D.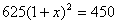
 ?若能,求出此时t的值;若不能,请说明理由.
?若能,求出此时t的值;若不能,请说明理由.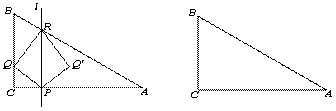
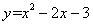 经过A、B、C三点,点P(1,k)在直线BC:y=x
经过A、B、C三点,点P(1,k)在直线BC:y=x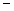 3上,若点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
3上,若点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.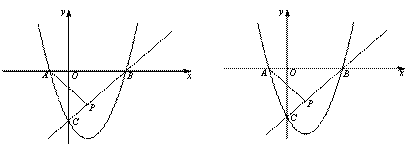
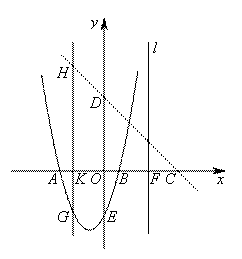
 ,圆心距为4.若
,圆心距为4.若 ,则两圆( )
,则两圆( )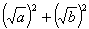 =
= +
+ +
+ 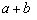 ≥
≥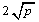 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值 (3)探索应用:如图2,已知A为反比例函数
(3)探索应用:如图2,已知A为反比例函数 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.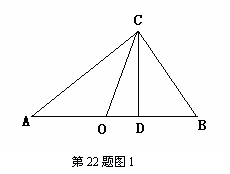
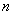 是正整数,则奇数可以用代数式
是正整数,则奇数可以用代数式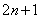 来表示.
来表示.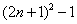 ;
;