题目内容
已知抛物线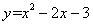
经过A、B、C三点，点P（1，k）在直线BC：y=x
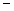3上，若点M在x轴上，点N在抛物线上，是否存在以A、M、N、P为顶点的四边形为平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．
 |
解：满足条件坐标为：
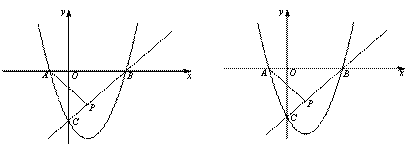
思路分析：A、M、N、P四点中点A、点P为顶点，则AP可为平行四边形边、对角线；
(1)如图，当AP为平行四边形边时，平移AP；
∵点A、P纵坐标差为2 ∴点M、N纵坐标差为2；
∵点M的纵坐标为0 ∴点N的纵坐标为2或-2
①当点N的纵坐标为2时
解：
得
又∵点A、P横坐标差为2 ∴点M的坐标为： 、
②当点N的纵坐标为-2时
解：
得
又∵点A、P横坐标差为2 ∴点M的坐标为： 、
(2)当AP为平行四边形边对角线时； 设M5（m,0）
MN一定过AP的中点（0，-1）
则N5（-m，-2），N5在抛物线上 ∴
（负值不符合题意，舍去）
∴
∴
综上所述:
符合条件点P的坐标为：
练习册系列答案
相关题目
,则
的值为( )
B．
C．
D．无法确定
”表示：每抛掷两次，就有一次正面朝上．
”表示：随着抛掷次数的增加，“抛出朝上点数是1”这一事件的频率是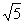
个单位长度的速度沿射线DA向上平移，直至正方形的顶点C落在y轴上时停止运动．在运动过程中，设正方形落在y轴右侧部分的面积为S，求S关于平移时间t（秒）的函数关系式，并写出相应的自变量t的取值范围．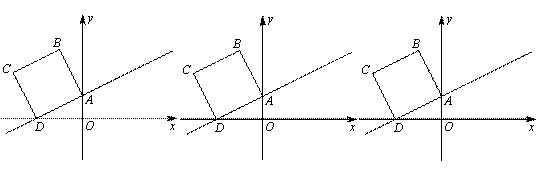
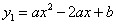经过A(-1，0)，C(2，
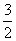)两点，
，求y2与x的函数关系式，
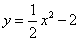的顶点，点B的坐标为
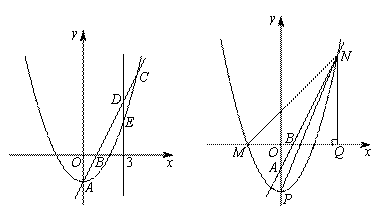（3）如图2，将抛物线C1向下平移m（m>0）个单位得到抛物线C2，且抛物线C2的顶点为P，交x轴负半轴于点M，交射线AB于点N，NQ⊥x轴于点Q，当NP平分∠MNQ时，求m的值．