题目内容
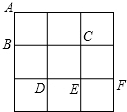 如图,在3×3方格纸中,点A、B、C、D、E、F分别位于小正方形的格点上.从A、D、
如图,在3×3方格纸中,点A、B、C、D、E、F分别位于小正方形的格点上.从A、D、E、F四个点中任意选取两个不同的点,以所取得这两个点与点B、C为顶点画四边形,则所画四边形是平行四边形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法,平行四边形的判定
专题:计算题
分析:列表得出所有等可能的情况数,找出能构成平行四边形的情况数,即可求出所求的概率.
解答:解:列表如下:
所有等可能的情况有12种,其中能构成平行四边形的有(E,A);(F,D);(A,E);(D,F)共4种,
则P=
=
.
故选B
| A | D | E | F | |
| A | --- | (D,A) | (E,A) | (F,A) |
| D | (A,D) | --- | (E,D) | (F,D) |
| E | (A,E) | (D,E) | --- | (F,E) |
| F | (A,F) | (D,F) | (E,F) | --- |
则P=
| 4 |
| 12 |
| 1 |
| 3 |
故选B
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 将一块直尺与一块三角板如图2放置,若∠1=45°,则∠2的度数为( )
将一块直尺与一块三角板如图2放置,若∠1=45°,则∠2的度数为( )| A、145° | B、135° |
| C、120° | D、115° |
已知
是二元一次方程组
的解,则
的算术平方根为( )
|
|
| m+3n |
| A、±3 | ||
| B、3 | ||
C、
| ||
D、±
|
已知分式
有意义,则x的取值范围是( )
| 3 |
| x-2 |
| A、x≥2 | B、x≥3 |
| C、x≠2 | D、x≠3 |
我市某一周每天最高气温统计如下:25,28,29,29,30,29,28(单位:℃).则这组数据的极差与众数分别是( )
| A、2,28 | B、5,29 |
| C、2,27 | D、3,28 |
-5的相反数是( )
A、
| ||
B、-
| ||
| C、-5 | ||
| D、5 |
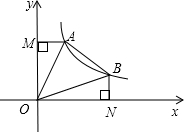 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y= 为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下:
为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下: