题目内容
8.有四张形状、大小和质地相同的卡片A、B、C、D,正面分别写有一个正多边形,把四张卡片洗匀后正面朝下放在桌面上,从中随机抽取一张(不放回),接着再随机抽取一张.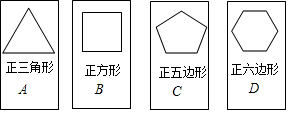
(1)请你用画树形图或列表的方法列举出可能出现的所有结果(用A、B、C、D表示);
(2)如果在(1)中各种结果被选中的可能性相同,求两次抽取的正多边形对称轴条数之和为奇数的概率.
分析 (1)列出图表即可得到所有的可能情况;
(2)根据轴对称的定义确定两次抽取的正多边形对称轴条数之和为奇数的结果,然后根据概率公式列式计算即可得解.
解答 解:(1)列表得:
| A | B | C | D | |
| A | BA | CA | DA | |
| B | AB | CB | DB | |
| C | AC | BC | DC | |
| D | AD | BD | CD |
(2)∵两次抽取的正多边形对称轴条数之和为奇数的情况有8种,
∴P(两次抽取的正多边形对称轴条数之和为奇数)=$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
16.对多项式x2-2x+1因式分解,结果正确的是( )
| A. | (x+1)2 | B. | (x+1)(x-1) | C. | (x-1)2 | D. | (x+1)(x-2) |
3.郑州已经正式被定为国家中心城市!作为郑州发展的核心,郑州机场2016年全年完成旅客吞吐量2076万次,同比增长20%,将数据2076万用科学记数法表示为( )
| A. | 2.076×108 | B. | 2076×106 | C. | 0.2076×108 | D. | 2.076×107 |
13.下列运算正确的是( )
| A. | 2xy-3xy=-1 | B. | x5÷x=x5 | C. | m3•m2=m6 | D. | (-m3n4)2=m6n8 |
 如图,已知AF分别与BD、CE交于点G、H,∠1=52°,∠2=128°.
如图,已知AF分别与BD、CE交于点G、H,∠1=52°,∠2=128°.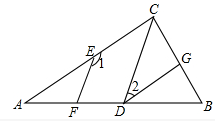 已知:如图,EF∥CD,∠1+∠2=180°.
已知:如图,EF∥CD,∠1+∠2=180°.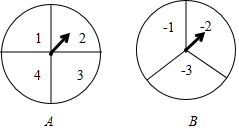 爸爸下班回家呆了一张同事送的《加勒比海盗5》的电影票,结果两小儿子都想要去看,于是爸爸提议用如图所示的两个转盘(其中转盘A被等分成4个扇形,且4个扇形内依次标有数字:1,2,3,4;转盘B被等分成3个扇形,且3个扇形内依次标有数字:-1,-2,-3)做游戏来决定谁去.
爸爸下班回家呆了一张同事送的《加勒比海盗5》的电影票,结果两小儿子都想要去看,于是爸爸提议用如图所示的两个转盘(其中转盘A被等分成4个扇形,且4个扇形内依次标有数字:1,2,3,4;转盘B被等分成3个扇形,且3个扇形内依次标有数字:-1,-2,-3)做游戏来决定谁去.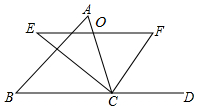 如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.