题目内容
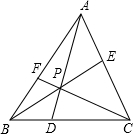已知P为△ABC内任意一点，连AP，BP，CP并延长分别交对边于D，E，F．求证：（1）
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
（2）
| AP |
| AD |
| BP |
| PE |
| CP |
| PF |
分析：（1）第一问可由三角形的面积入手，即△PBC+△PAC+△PAB=△ABC，通过化简可得面积与线段之间的关系，进而即可求解．
（2）由（1）中得出
+
+
=1，则其中至少有一个不大于
，可设
≤
，即3AD≤PD，而AD=AP+PD，进而通过证明即可得出结论．
（2）由（1）中得出
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| 1 |
| 3 |
| PD |
| AD |
| 1 |
| 3 |
解答：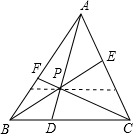
解：（1）由面积概念得：
S△PBC+S△PAC+S△PAB=S△ABC①
整理等式得：
+
+
=1，②
由面积概念得：
=
，
=
，
∴
=
，
即
=
③
同理得：
=
④
=
⑤
把式③、④、⑤、代入式②得：
+
+
=1；
（2）由
+
+
=1，知
，
，
中至少有一个不大于
，
不妨设
≤
即3PD≤AD．
而AD=AP+PD，
∴AP≥2PD，
∴
≥2，即
不小于2，
同理可证三式中至少有一个不大于2．
解：（1）由面积概念得：S△PBC+S△PAC+S△PAB=S△ABC①
整理等式得：
| S△PBC |
| S△ABC |
| S△PAC |
| S△ABC |
| S△PAB |
| S△ABC |
由面积概念得：
| S△PDC |
| S△ADC |
| PD |
| AD |
| S△PDB |
| S△ADB |
| PD |
| AD |
∴
| S△PDC+S△PDB |
| S△ADC+S△ADB |
| PD |
| AD |
即
| S△PBC |
| S△ABC |
| PD |
| AD |
同理得：
| S△PAC |
| S△ABC |
| PE |
| BE |
| S△PAB |
| S△ABC |
| PF |
| CF |
把式③、④、⑤、代入式②得：
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
（2）由
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| 1 |
| 3 |
不妨设
| PD |
| AD |
| 1 |
| 3 |
而AD=AP+PD，
∴AP≥2PD，
∴
| AP |
| PD |
| AP |
| PD |
同理可证三式中至少有一个不大于2．
点评：本题主要考查了三角形的面积比与对应边的比值之间的关系，能够熟练掌握其内在联系，并能求解一些比较复杂的问题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
18、如图，已知D为△ABC内任一点，求证：∠BDC＞∠ABD．
(AB＋BC＋AC)．
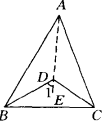
如图，已知D为△ABC内任一点，求证：∠BDC＞∠ABD．