题目内容
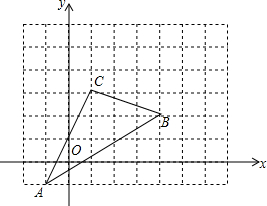
2．
如图，方格纸中每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图所示．（1）在图中作出△ABC关于y轴对称的△A1B1C1，并直接写出点A1的坐标．
（2）将△ABC绕点O顺时针旋转90°得△A2B2C2，在图中作出△A2B2C2，并计算点A旋转到点A2所经过的路径长．
分析 （1）直接利用轴对称点的性质得出对应点位置进而得出答案；
（2）直接利用旋转的性质得出对应点位置进而得出答案．
解答 
解：（1）如图所示：△A1B1C1，即为所求，
A1（-3，3）；
（2）如图所示：△A2B2C2，即为所求，
则OA=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$，
故点A旋转到点A2所经过的路径长为：$\frac{90π×3\sqrt{2}}{180}$=$\frac{3\sqrt{2}}{2}$π．
点评 此题主要考查了旋转变换和轴对称变换，正确得出对应点位置是解题关键．
练习册系列答案
相关题目
12．本溪电视台某日发布的当天的天气预报，我市Ⅱ各地区当天最高气温（℃）统计如表：
那么这些城市当天的最高气温的众数和中位数分别是13℃，13℃．
| 气温（℃） | 10 | 11 | 12 | 13 | 14 | 15 | 17 |
| 频数 | 1 | 1 | 1 | 3 | 2 | 2 | 1 |
如图，三角形ABC在直角坐标系中，
7．有7位歌手（1至7号）参加一场歌唱比赛，由500名大众评委现场投票决定歌手名次，根据年龄将大众评委分为5组，各组的人数如下：
（Ⅰ）为了调查评委对7位歌手的支持状况，现用分层抽样方法从各组中抽取若干评委，其中从B组中抽取了6人．请将其余各组抽取的人数填入下表．
（Ⅱ）在（Ⅰ）中，若A，B两组被抽到的评委中各有2人支持1号歌手，现从这两组被抽到的评委中分别任选1人，求这2人都支持1号歌手的概率．
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | 6 |
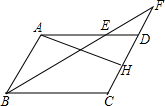如图，在?ABCD中，AB=4，AD=6，∠ABC的平分线交AD于点E，交CD的延长线于点F．