题目内容
7.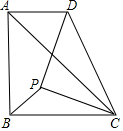 如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为$\sqrt{2}$.
如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为$\sqrt{2}$.
分析 作PF⊥BC于点F,延长FP交AD于点E,证△PCF≌△DPE得PF=DE、PE=CF,从而得PE=CF=4-x,根据四边形ABCD的面积求得AD的长,据此知AE=BF=2-x、FC=BC-BF=4-(2-x)=2+x,从而得2+x=4-x,求得x的值,由勾股定理得出答案.
解答 解:如图,作PF⊥BC于点F,延长FP交AD于点E,
∵AD∥BC,
∴∠PFC=∠DEP=90°,
∴∠CPF+∠PCF=90°,
∵∠DPC=90°,
∴∠CPF+∠DPE=90°,
∴∠PCF=∠DPE,
在△PCF和△DPE中,
∵$\left\{\begin{array}{l}{∠PCF=∠DPE}\\{∠PFC=∠DEP}\\{PC=DP}\end{array}\right.$,
∴△PCF≌△DPE(AAS),
∴PF=DE、PE=CF,
设PF=DE=x,则PE=CF=4-x,
∵S四边形ABCD=$\frac{1}{2}$(AD+BC)•AB=12,
∴$\frac{1}{2}$×(AD+4)×4=12,解得AD=2,
∴AE=BF=2-x,
∴FC=BC-BF=4-(2-x)=2+x,
可得2+x=4-x,解得x=1,
∴BP=$\sqrt{B{F}^{2}+P{F}^{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题主要考查全等三角形的判定与性质、矩形的性质、四边形的面积及勾股定理,熟练掌握全等三角形的判定与性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列运算正确的是( )
| A. | (-3)2=-9 | B. | (-1)2017×(-1)=1 | C. | -9÷3=3 | D. | -|-1|=1 |
18.下列四个命题:①坐标平面内的点与有序数对一一对应;②若a大于0,b不大于0,则点P(-a,-b)在第三象限;③在x轴上的点的纵坐标都为0;④当m=0时,点P(m2,-m)在第四象限.其中,是真命题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.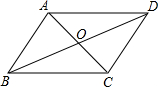 如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
 如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )| A. | AB=AD,BC=CD | B. | AO=OC,BO=DO | C. | AO⊥OD | D. | AO⊥AB |
2.把点A(2,-3)先向上平移2个单位,再向左平移3个单位得到的点的坐标为( )
| A. | (4,0) | B. | (-1,-1) | C. | (5,-1) | D. | (-1,-5) |
12.将直线y=2x-4向上平移5个单位长度后,所得直线的表达式是( )
| A. | y=2x-9 | B. | y=2x-5 | C. | y=2x+5 | D. | y=2x+1 |
19. 如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=( )
如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=( )
 如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=( )
如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
16.下列事件中,属于随机事件的是( )
| A. | 若a是实数,则|a|≥0 | B. | 在地球上,抛出的篮球会落下 | ||
| C. | 打开电视机,正在播放广告 | D. | 从装有黑球,白球的袋里摸出红球 |
17.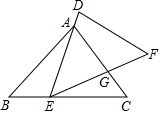 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AD}{AE}$=$\frac{GF}{GE}$ | C. | $\frac{AG}{AC}$=$\frac{EG}{EF}$ | D. | $\frac{ED}{EF}$=$\frac{EG}{EA}$ |