题目内容
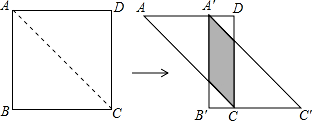
.如图,将边长为 6 的正方形 ABCD 沿其对角线 AC 剪开,再把△ABC 沿着 AD 方向平移,得到
△A′B′C′,当两个三角形重叠部分为菱形时,则 AA′为 .
12﹣6 .
.
【考点】菱形的性质;正方形的性质;平移的性质.
【分析】利用菱形的性质结合正方形的性质得出 A′D=DF,AA′=A′E,进而利用勾股定理得出答案.
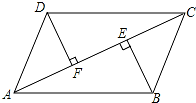
【解答】解:如图所示:∵四边形 A′ECF 是菱形,
∴A′E=EC=FC=A′F,
∵边长为 6 的正方形 ABCD 沿其对角线 AC 剪开,再把△ABC 沿着 AD 方向平移,
∴∠A=∠ACD=45°,
∴AD=DC,则 A′D=DF,AA′=A′E,
∴设 A′E=x,则 A′D=DF=6﹣x,A′F=x, 故在 Rt△A′DF 中, x2=(6﹣x)2+(6﹣x)2,
 解得:x1=12﹣6 ,x2=12+6
解得:x1=12﹣6 ,x2=12+6  >6(不合题意舍去), 故 AA′为:12﹣6 .
>6(不合题意舍去), 故 AA′为:12﹣6 .
故答案为:12﹣6 .
【点评】此题主要考查了菱形的性质和正方形的性质、勾股定理等知识,得出 A′D=DF,AA′=A′E
是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
反比例函数 的图象上有两点M,N,那么图中阴影部分面积最大的是
的图象上有两点M,N,那么图中阴影部分面积最大的是
|
|
|
|
|
| ||||
| A. B. C. D. |
 3 D.±
3 D.±

 B、
B、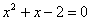
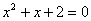 D、
D、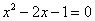
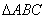 是等边三角形.
是等边三角形. (用尺规作图,保留作图痕迹,不写作法);
(用尺规作图,保留作图痕迹,不写作法);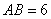
 ,求⊙
,求⊙