题目内容
如图,▱ABCD的周长为36.对角线AC,BD相交于点O.点E是CD的中点.BD=12.则△DOE的周长为 .

15【解析】∵▱ABCD 的周长为36,∴BC+CD=18.
的周长为36,∴BC+CD=18.
∵四边形ABCD为平行四边形,
∴O是BD的中点,∴OD=6,
又∵E是CD的中点,
∴OE是△BCD的中位线,
∴OE= BC,DE=
BC,DE= CD,∴OE+DE=9,
CD,∴OE+DE=9,
∴△DOE的周长=OD +OE+DE=6+9=15.
+OE+DE=6+9=15.
答案:15

练习册系列答案
相关题目
为了迎接今年的国庆节,八(3)、八(5)班举行跳绳比赛,各班参赛选手每分钟跳绳的次数经统计计算后填入下表:
| 班级 | 参加人数 (人) | 中位数 (次/分) | 方差 | 平均次数 (次/分) |
| 八(3) | 45 | 171 |
| 155 |
| 八(5)班 | 45 | 169 | 16.32 | 155 |
某同学根据表格得出如下结论:①八(3)、八(5)班跳绳的平均水平相同.②若跳绳速度多于每分钟170次的算作优秀,则八(3)班优秀人数不少于八(5)班.③八(5)班跳绳比赛成绩波动情况比八(3)班成绩的波动大.上述结论正确的个数有
( )
A.3个 B.2个 C.1个 D.0个
 B.m=
B.m= 班
班 9.54
9.54
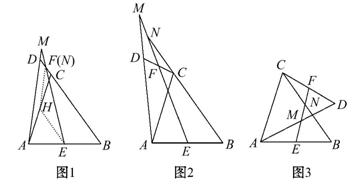
 ,BC,BA延长线上的点,四边形ADEF为平行四边形.求证:AD=BF.
,BC,BA延长线上的点,四边形ADEF为平行四边形.求证:AD=BF.
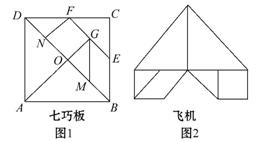
 BCD进行分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 .
BCD进行分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 .