Question

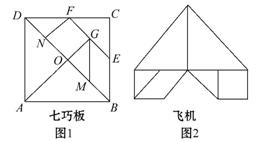
对正方形ABCD进行分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为　　　　.

Answer 1

14

【解析】连接AC,四边形ABCD是正方形,AC⊥BD,E,F分别是BC,CD的中点,EF∥BD,AC⊥EF,CF=CE,△EFC是等腰直角三角形,直线AC是△EFC底边上的高所在直线,根据等腰三角形“三线合一”,AC必过EF的中点G,点A,O,G和C在同一条直线上,OC=OB=OD,OC⊥OB,FG是△DCO的中位线,OG=CG=OC,M,N分别是OB,OD的中点,OM=BM=OB,ON=DN=OD,OG=OM=BM=ON=DN=BD,等腰直角三角形GOM的面积为1,OM·OG=OM²=1,OM=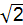,BD=4OM=4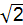,2AD²=BD²=32,AD=4,图2中飞机面积等于图1中多边形ABEFD的面积,飞机面积=正方形ABCD的面积-三角形CEF的面积=16-2=14.