题目内容
对任意实数x，多项式x2-4x+7的值是一个（ ）
| A、正数 | B、负数 |
| C、非负数 | D、无法确定 |
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：首先将多项式x2-4x+7配方，然后即可确定正确的选项．
解答：解：∵x2-4x+7=x2-4x+4+3=（x-2）2+3＞0，
∴对任意实数x，多项式x2-4x+7的值是一个正数，
故选A．
∴对任意实数x，多项式x2-4x+7的值是一个正数，
故选A．
点评：本题考查了配方法：配方法的理论依据是公式a2±2ab+b2=（a±b）2．也考查了非负数的性质．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
与方程组
有相同解的方程是（ ）
|
| A、x+y=3 | ||
| B、2x+3y+4=0 | ||
C、3x+
| ||
| D、x-y=1 |
已知x=2是方程2（x-3）+1=x+m的解，则m-1的值是（ ）
| A、3 | B、-3 | C、-4 | D、4 |
方程3y+5x=27与下列的方程所组成的方程组的解是
（ ）
|
| A、4x+6y=-6 |
| B、4x+7y-40=0 |
| C、2x-3y=13 |
| D、以上答案都不对 |
某鞋店试销一款女鞋，试销期间对不同颜色鞋的销售情况统计如下表：
若将上面的数据制成扇形统计图，则棕色鞋的数量所在扇形的圆心角的度数为（ ）
| 颜色 | 黑色 | 棕色 | 白色 | 红色 |
| 销售量（双） | 6 | 15 | 40 | 19 |
| A、87.5° |
| B、85.5° |
| C、76.5° |
| D、67.5° |
若点A（2-a，1-2a）关于y轴的对称点在第三象限，则a的取值范围是（ ）
A、a＜
| ||
| B、a＞2 | ||
C、
| ||
D、a＜
|
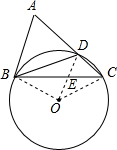已知如图，在△ABC中，∠ACB=45°，D为AC上一点，且∠ADB=60°，AB切△BCD的外切圆于B，求证：AD=2DC．