题目内容
P是△ABC内一点,AD、BE、CF过点P并且交边BC、CA、AB于D、E、F,则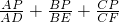 =________.
=________.
2
分析:将AD和PD看作△ABD和△PBD的底,由于两三角形在AD和PD上的高相等,则其面积比等于底的比,同理,S△CDP:S△ACD=DP:AD,可推知,S△BCP:S△ABC=DP:AD,同理有S△ABP:S△ABC=PF:CF,S△ACP:S△ABC=PE:BE,将三者相加即可得到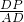 +
+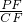 +
+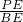 =(S△BCP+S△ABP+S△ACP):S△ABC=1,将原式变形,再求出
=(S△BCP+S△ABP+S△ACP):S△ABC=1,将原式变形,再求出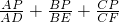 的比.
的比.
解答:证明:如图:∵S△BDP:S△ABD=DP:AD,
S△CDP:S△ACD=DP:AD,
∴(S△BDP+S△CDP):(S△ABD+S△ACD)=DP:AD,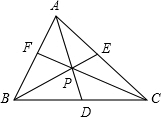
∴S△BCP:S△ABC=DP:AD①,
同理S△ABP:S△ABC=PF:CF②,
S△ACP:S△ABC=PE:BE③,
①+②+③,得
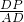 +
+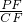 +
+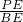 =(S△BCP+S△ABP+S△ACP):S△ABC=1.
=(S△BCP+S△ABP+S△ACP):S△ABC=1.
∴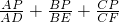
=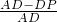 +
+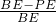 +
+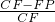
=1-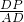 +1-
+1-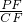 +1-
+1-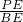
=3-(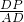 +
+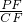 +
+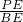 )
)
=3-1
=2.
故答案为2.
点评:本题考查了三角形的面积,将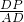 、
、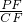 、
、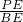 转化为面积的比是解题的关键.
转化为面积的比是解题的关键.
分析:将AD和PD看作△ABD和△PBD的底,由于两三角形在AD和PD上的高相等,则其面积比等于底的比,同理,S△CDP:S△ACD=DP:AD,可推知,S△BCP:S△ABC=DP:AD,同理有S△ABP:S△ABC=PF:CF,S△ACP:S△ABC=PE:BE,将三者相加即可得到
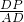 +
+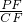 +
+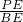 =(S△BCP+S△ABP+S△ACP):S△ABC=1,将原式变形,再求出
=(S△BCP+S△ABP+S△ACP):S△ABC=1,将原式变形,再求出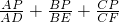 的比.
的比.解答:证明:如图:∵S△BDP:S△ABD=DP:AD,
S△CDP:S△ACD=DP:AD,
∴(S△BDP+S△CDP):(S△ABD+S△ACD)=DP:AD,

∴S△BCP:S△ABC=DP:AD①,
同理S△ABP:S△ABC=PF:CF②,
S△ACP:S△ABC=PE:BE③,
①+②+③,得
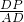 +
+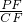 +
+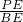 =(S△BCP+S△ABP+S△ACP):S△ABC=1.
=(S△BCP+S△ABP+S△ACP):S△ABC=1.∴
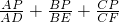
=
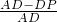 +
+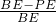 +
+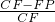
=1-
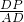 +1-
+1-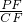 +1-
+1-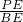
=3-(
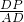 +
+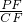 +
+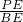 )
)=3-1
=2.
故答案为2.
点评:本题考查了三角形的面积,将
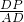 、
、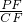 、
、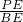 转化为面积的比是解题的关键.
转化为面积的比是解题的关键. 
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
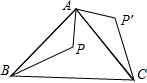 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=

 如图,在△ABC中,AB=AC,点D是△ABC内一点,点E和点D在AC的异侧,并且AD=AE,∠AED=∠ACB,则BD=CE吗?请说明理由.
如图,在△ABC中,AB=AC,点D是△ABC内一点,点E和点D在AC的异侧,并且AD=AE,∠AED=∠ACB,则BD=CE吗?请说明理由.