题目内容
4.已知二次函数y=x2-4x+3(1)将其化成y=a(x-h)2+k的形式;
(2)写出这个二次函数图象的开口方向、对称轴方程和顶点坐标;
(3)求出这个二次函数的图象与两坐标轴的交点;
(4)画出函数的图象,并指出y>0及y<0时x的范围.
分析 (1)根据配方法即可解决.
(2)由a的值确定开口方向,根据顶点式即可写出对称轴、顶点坐标.
(3)令y=0解方程即可.
(4)由顶点、以及与x轴交点即可画出图象,由图象直接可以写出y>0及y<0时x的范围.
解答 解:(1)y=(x-2)2-1,
(2)开口向上、对称轴x=2,顶点坐标(2,-1)
(3)令y=0,则x2-4x+3=0解得:x=1或3,所以与x轴交点为(1,0)和(3,0),
(4)图象如图1,
由图象可知y>0时,x<1或x>3
y<0时,1<x<3.
点评 本题考查用二次函数有关知识,要求会用配方法求对称轴、顶点坐标,会求二次函数与x轴交点坐标,会利用图象确定y>0及y<0时x的范围.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 8的立方根是±2 | B. | -1不存在立方根 | ||
| C. | 2的算术平方根是$±\sqrt{2}$ | D. | -25不存在平方根 |
 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以lcm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发.
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以lcm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发. 如图,AB∥CD交AD、BC于点E,AE=3,ED=6,AB=4,那么CD=8.
如图,AB∥CD交AD、BC于点E,AE=3,ED=6,AB=4,那么CD=8. 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为2.
如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为2.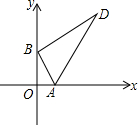 Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最大值和最小值的乘积为48.
Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最大值和最小值的乘积为48.