题目内容
18.(1)知识再现如图(1):若点A,B在直线l同侧,A,B到l的距离分别是3和2,AB=4,现在直线l上找一点P,使AP+BP的值最小.作法如下;作点A关于直线l的对称点A′,连接BA′,与直线l的交点就是所求的点P,线段BA′的长度即为AP+BP的最小值,请你求出这个最小值.
(2)实践应用
①如图(2),⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是2$\sqrt{3}$;
②如图(3),Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,$\sqrt{3}$),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为$\sqrt{7}$;
③如图(4),菱形ABCD中AB=2,∠A=120°,点P,Q,K,分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为2;
④如图(5),在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.
(3)拓展延伸
如图(6),在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD,保留作图痕迹,不必写出作法.
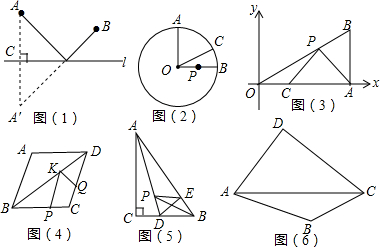
分析 (1)连接AB,过B作BK⊥AA′于K,求出BK,根据勾股定理求出A′B即可;
(2)①延长AO交⊙O于E,连接CE交OB于P,连接AP,此时PA+PC值最小,解直角三角形求出CE即可;
②过A作AW⊥OB于W,并延长AW到E,使AW=WE,连接CE交OB于P,连接AP,则此时PA+PC值最小,过E作EF⊥OA于F,求出AW,求出AE,EF,即可求出CE,根据CE能得出答案;
③过Q作QM⊥AB,交AB于M,连接PM,交BD于K,则此时PK+QK的值最小,过C作CN⊥AB于N,求出CN即可;
④求出P和D重合时符合题意,求出BC,即可得出答案;
(3)根据轴对称作B点关于AC的对称点E,延长DE交AC于P,则P为所求.
解答 解:(1)
连接AB,过B作BK⊥AA′于K,
∵AB=4,AC=3,AK=1,
∴在Rt△AKB中,BK2=15,
∵KA′=5,
∴在Rt△A′KB中,BA′=$\sqrt{40}$=2$\sqrt{10}$;
(2)①如图(2),
延长AO交⊙O于E,连接CE交OB于P,连接AP,此时PA+PC值最小,
连接AC,
∵AE为直径,
∴∠ACB=90°,AE=2×2=4,
∵∠AOC=60°,
∴∠E=30°,
∴AC=$\frac{1}{2}$AE=2,
由勾股定理得:CE=2$\sqrt{3}$,
即PA+PC=CE=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$;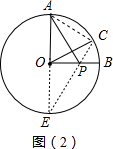
②如图(3),
过A作AW⊥OB于W,并延长AW到E,使AW=WE,连接CE交OB于P,连接AP,则此时PA+PC值最小,
过E作EF⊥OA于F,
∵B(3,$\sqrt{3}$),
∴tan∠AOB=$\frac{\sqrt{3}}{3}$,
∴∠BOA=30°,
∴∠B=60°,
∴∠BAW=30°,∠CAW=60°,
∴AF=$\frac{1}{2}$AE=AW,
∵B(3,$\sqrt{3}$),
∴OA=3,AB=$\sqrt{3}$,
由勾股定理得:OB=2$\sqrt{3}$,
由三角形面积公式得:AB×OA=OB×AW,
∴AW=$\frac{3×\sqrt{3}}{2\sqrt{3}}$=$\frac{3}{2}$,
∴AE=2AW=3,AF=$\frac{3}{2}$,
由勾股定理得:EF=$\sqrt{{3}^{2}-(\frac{3}{2})^{2}}$=$\frac{3\sqrt{3}}{2}$,
∵OC=1,AF=$\frac{3}{2}$,OA=3,
∴CF=$\frac{1}{2}$,
由勾股定理得:CE=$\sqrt{(\frac{3\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}$=$\sqrt{7}$,
即PA+PC的最小值是$\sqrt{7}$,
故答案为:$\sqrt{7}$;
③如图(4),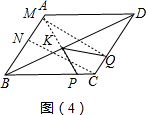
过Q作QM⊥AB,交AB于M,连接PM,交BD于K,则此时PK+QK的值最小,过C作CN⊥AB于N,
∵四边形ABCD是菱形,
∴AB=BC=2,AB∥CD,
∴CN=QM,
∵在Rt△CNB中,∠CNB=90°,BC=2,∠CNB=90°,
∴CN=$\sqrt{3}$,
∴QM=CN=$\sqrt{3}$,
即PK+QK的最小值是$\sqrt{3}$,
故答案为:$\sqrt{3}$;
④如图(5),
连接CE,交AD于F,
∵沿着AD折叠C和E重合,
∴AD垂直平分CE,即当P和D重合时,EP+BP值最小,即△PEB的周长最小,
∵CD=$\sqrt{3}$,
∴DE=CD=$\sqrt{3}$,
∵∠B=60°,∠DEB=90°,
∴BE=1,BD=2,
∴PB+PE=BC=2+$\sqrt{3}$,
∴△PEB的周长为PE+PB+BE=2+$\sqrt{3}$+1=3+$\sqrt{3}$,
故答案为:3+$\sqrt{3}$;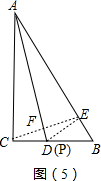
(3)如图: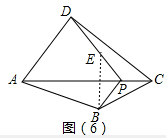
点评 本题考查了轴对称的性质,折叠的性质,勾股定理,菱形的性质的应用,能找出符合条件的P点事解此题的关键,题目求解过程类似,但是有一定的难度.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案①射线AB和射线BA是同一条射线.
②将一根细木条固定在墙上,至少需要钉两个钉子,其理论依据是:两点之间线段最短.
③两点间的连线的长度叫做这两点间的距离.
④表示北偏东70°方向、南偏东20°方向的两条射线所夹的角为直角.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 日期 | 1月7日 | 1月8日 | 1月9日 | 1月10日 |
| 最高气温 | 5℃ | 5℃ | 4℃ | 7℃ |
| 最低气温 | -5℃ | -3℃ | -4℃ | -5℃ |
| A. | 1月7日 | B. | 1月8日 | C. | 1月9日 | D. | 1月10日 |
| A. | 日光灯管厂要检测一批灯管的使用寿命 | |
| B. | 了解嘉兴市每天的流动人口数 | |
| C. | 了解浙江省城市居民日平均用水量 | |
| D. | 旅客上飞机前的安全检查 |
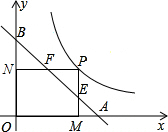 如图,双曲线y=$\frac{1}{2x}$(x>0)上有一动点P,作PM⊥x轴于M,PN⊥y轴于N,直线AB:y=-x+1分别交PM、PN于点E、F.
如图,双曲线y=$\frac{1}{2x}$(x>0)上有一动点P,作PM⊥x轴于M,PN⊥y轴于N,直线AB:y=-x+1分别交PM、PN于点E、F.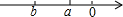 如图,a,b所在数轴的位置,化简下列各式:
如图,a,b所在数轴的位置,化简下列各式: 已知:如图,点B、C分别在∠BAC的两条边上,BE和CD相交于点F,连接DE.求证:∠A+∠B+∠C+∠D+∠E=180°.
已知:如图,点B、C分别在∠BAC的两条边上,BE和CD相交于点F,连接DE.求证:∠A+∠B+∠C+∠D+∠E=180°.