题目内容
19.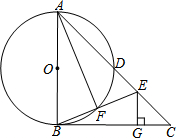 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.(1)求证:∠CBE=∠CAF;
(2)过点E作EG⊥BC于点G,若∠C=45°,CG=1,求⊙O的半径.
分析 (1)由BC切⊙O于点B,得到∠ABF+∠CBE=90°,由AB是⊙O的直径,得到∠ABF+∠BAF=90°,通过等量代换得到∠CBE=∠BAF,由已知条件∠BAC=2∠CBE,得到∠BAF+∠CAF=2∠CBE于是得到结论∠CBE=∠CAF;
(2)连接BD,证明△BED≌△BEG,得到ED=EG,由于∠C=∠CEG=45°,得到EG=CG=1,CE=$\sqrt{2}$,解直角三角形即可求得结果.
解答 解:(1)证明:BC切⊙O于点B,
∴∠ABF+∠CBE=90°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠ABF+∠BAF=90°,
∴∠CBE=∠BAF.
∵∠BAC=2∠CBE,
∴∠BAF+∠CAF=2∠CBE,
即∠CBE=∠CAF;
(2)如图,连接BD,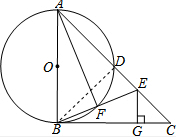
∵EG⊥BC于点G,
∴∠CBE+∠BEG=90°,
∵∠CAF+∠AEF=90°,
∴∠BEG=∠AEF,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BDE=∠BGE=90°,
∵BE=BE,
在△BED与△BEG中,$\left\{\begin{array}{l}{∠BEG=∠AEF}\\{∠BDE=∠BGE}\\{BE=BE}\end{array}\right.$,
∴△BED≌△BEG,
∴ED=EG,
∵∠C=∠CEG=45°,
∴EG=CG=1,CE=$\sqrt{2}$,
∴DE=1,
∴CD=1+$\sqrt{2}$,
在Rt△ABC中,∠ABC=90°,∠C=45°,
∴∠BAC=45°,
∴AD=BD=CD=1+$\sqrt{2}$,
∴AB=2+$\sqrt{2}$,
∴⊙O的半径为$\frac{{2+\sqrt{2}}}{2}$.
点评 本题考查了圆的切线的判定定理、圆周角定理、全等三角形的判定与性质,解直角三角形,正确的作出辅助线构造全等三角形是解题的关键.

北京市居民用水阶梯水价表 单位:元/立方米
| 分档水量 | 户年用水量 (立方米) | 水价 | 其中 | ||
| 自来水费 | 水资源费 | 污水 处理费 | |||
| 第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
| 第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
| 第三阶梯 | 260以上 | 9.00 | 6.07 | ||
| 车主的态度 | 百分比 |
| A.没有影响 | 4% |
| B.影响不大 | p |
| C.有影响 | 52% |
| D.影响很大 | m |
| E.不关心这个问题 | 10% |

(1)结合上述统计图表可得:p=24%,m=10%;
(2)根据以上信息,补全条形统计图;
(3)2014年1月末,某市有机动车的私家车车主约200 000人,根据上述信息,请你估计一下持有“影响不大”这种态度的车主约有多少人?
| A. | 300° | B. | 240° | C. | 180° | D. | 120° |