题目内容
9.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+y=2-a}\\{x+2y=3}\end{array}\right.$的解满足x-y>2,则a的取值范围是a<-3.分析 方程组两方程相减表示出x-y,代入已知不等式求出a的范围即可.
解答 解:$\left\{\begin{array}{l}{2x+y=2-a①}\\{x+2y=3②}\end{array}\right.$,
①-②得:x-y=-a-1,
代入不等式得:-a-1>2,
解得:a<-3.
故答案为:a<-3.
点评 此题考查了二元一次方程组的解,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
19.下列方程是一元二次方程的是( )
| A. | ax2=bx | B. | x2+3y-1=0 | C. | 3x2-2x+$\frac{1}{x}$=0 | D. | 2(x+1)(x-1)=x+5 |
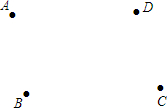 如图,A,B,C,D是四个鱼塘的位置,要用一个供水泵向这四个鱼塘供水,为了使供水管最短,供水泵应建在什么位置?画出图形并说明理由.
如图,A,B,C,D是四个鱼塘的位置,要用一个供水泵向这四个鱼塘供水,为了使供水管最短,供水泵应建在什么位置?画出图形并说明理由.