题目内容
20．解不等式组$\left\{\begin{array}{l}{x-2＜4}\\{2x-1＞1}\end{array}\right.$，并将解集表示在数轴上．分析 先求出两个不等式的解集，再求其公共解．
解答 解$\left\{\begin{array}{l}{x-2＜4①}\\{2x-1＞1②}\end{array}\right.$
解不等式①，得x＜6，
解不等式②，得x＞1，
在数轴上表示如下：
所以原不等式组的解是1＜x＜6．
点评 本题考查了解一元一次不等式组，在数轴上表示不等式组的解集的应用，能根据不等式的解集求出不等式组的解集是解此题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
10．
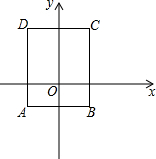如图，四边形ABCD是长方形，AB=3，AD=4．已知A（-$\frac{3}{2}$，-1），则点C的坐标是（ ）
如图，四边形ABCD是长方形，AB=3，AD=4．已知A（-$\frac{3}{2}$，-1），则点C的坐标是（ ）| A． | （-3，$\frac{3}{2}$） | B． | （$\frac{3}{2}$，-3） | C． | （3，$\frac{3}{2}$） | D． | （$\frac{3}{2}$，3） |
11．下列等式从左到右的变形是因式分解的是（ ）
| A． | 2a3b=a2•2ab | B． | （x+3）（x-3）=x2-9 | ||
| C． | 2x2+4x-3=2x（x+2）-3 | D． | ax+ay=a（x+y） |
8．
如图：AB∥CD，直线MN与AB交于E，过点E作直线HE⊥MN，∠1=130°，则∠2等于（ ）
如图：AB∥CD，直线MN与AB交于E，过点E作直线HE⊥MN，∠1=130°，则∠2等于（ ）| A． | 50° | B． | 40° | C． | 30° | D． | 60° |