题目内容
10.如图1,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6,∠OMN=45°,点P从点O出发,以每秒钟1个单位的速度沿折线ONM运动,设点P运动时间为t (s),△POM的面积S.(1)当S=$\frac{1}{2}$△OMN时,请直接写出点P的坐标;
(2)当t=6+5$\sqrt{2}$时,直线x=$\frac{3}{4}$上有一个动点C和y轴上有一动点D,当PD+DC+OC值最小时,求C、D两点的坐标及此时PD+DC+OC最小值;
(3)如图3,有一个和△NOM全等的△AOB,现将△AOB绕点O顺时针旋转a°(0<a<180)形成△A′OB′,直线OB′与直线MN交于点F,直线A′B′交直线MN于点E,在旋转过程中△EFB′为等腰三角形时,请直接写出a的度数与B′点的横坐标的平方.
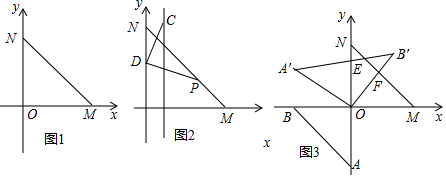
分析 (1)当S=△OMN面积的一半时,分两种情况进行讨论:①点P在ON上;点P在MN上,分别求得点P的坐标;
(2)先根据当t=6+5$\sqrt{2}$时,ON+NP=6+5$\sqrt{2}$,NP=5$\sqrt{2}$,PM=$\sqrt{2}$,求得点P的坐标为(5,1),再作点P关于y轴对称的点P',作点O关于直线x=$\frac{3}{4}$的对称点O',则P'(-5,1),O'($\frac{3}{2}$,0),连接O'P',交y轴于点D,交直线x=$\frac{3}{4}$于点C,则此时PD+DC+OC值最小,等于线段O'P'的长,运用待定系数法求得直线O'P'的解析式为y=-$\frac{2}{13}$x+$\frac{3}{13}$,进而得到C、D两点的坐标及此时PD+DC+OC最小值;
(3)根据旋转过程中△EFB′为等腰三角形,需要分三种情况讨论:当EB'=EF时,当B'E=B'F时,当FE=FB'时,分别求得a的度数与B′点的横坐标的平方.
解答 解:(1)分两种情况讨论:
①如图1,当点P在ON上时,根据S=△OMN面积的一半,可得点P为NO的中点,
∵OM=6,∠OMN=45°,
∴△MON是等腰直角三角形,
∴ON=6,
∴OP=3,
∴P(0,3);
②如图1,当点P在MN上时,根据S=△OMN面积的一半,可得点P为NM的中点,
∵△MON是等腰直角三角形,OM=ON=6,
∴P(3,3);
综上所述,点P的坐标为(0,3)或(3,3);
(2)∵ON=6,
∴当t=6+5$\sqrt{2}$时,ON+NP=6+5$\sqrt{2}$,NP=5$\sqrt{2}$,PM=$\sqrt{2}$,
∴点P的坐标为(5,1),
如下图,作点P关于y轴对称的点P',作点O关于直线x=$\frac{3}{4}$的对称点O',则P'(-5,1),O'($\frac{3}{2}$,0),
连接O'P',交y轴于点D,交直线x=$\frac{3}{4}$于点C,则此时PD+DC+OC值最小,等于线段O'P'的长,
设直线O'P'的解析式为y=kx+b,则
$\left\{\begin{array}{l}{1=-5k+b}\\{0=\frac{3}{2}k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{13}}\\{b=\frac{3}{13}}\end{array}\right.$,
∴直线O'P'的解析式为y=-$\frac{2}{13}$x+$\frac{3}{13}$,
∴当x=$\frac{3}{4}$时,y=$\frac{3}{26}$,即C($\frac{3}{4}$,$\frac{3}{26}$);
当x=0时,y=$\frac{3}{13}$,即D(0,$\frac{3}{13}$);
此时PD+DC+OC=O'P'=$\sqrt{(\frac{3}{2}+5)^{2}+{1}^{2}}$=$\frac{\sqrt{173}}{2}$,
∴PD+DC+OC最小值为$\frac{\sqrt{173}}{2}$;
(3)①当EB'=EF时,∠B'=∠B'FE=∠MFO=45°,
∵∠FMO=45°,
∴此时∠MOF=90°,即点F与点N重合,即OF=ON,
故△EFB′不存在,不合题意;
②当B'E=B'F时,如图,过点B'作B'H⊥OM于H,过点F作FG⊥OM于G,则FG∥B'H,
∵∠EB'F=45°,
∴∠B'FE=∠MFO=67.5°=∠MFO,
又∵∠OMF=45°,
∴∠MOF=67.5°,
∴a的度数=∠BOB'=112.5°,
此时MF=MO=6,
∴Rt△MFG中,FG=MG=3$\sqrt{2}$,
∴OG=6-3$\sqrt{2}$,
由FG∥B'H,可得$\frac{OG}{OM}$=$\frac{FG}{B'H}$,即$\frac{6-3\sqrt{2}}{OH}$=$\frac{3\sqrt{2}}{B'H}$,
∴B'H=$\frac{3\sqrt{2}}{6-3\sqrt{2}}$OH=($\sqrt{2}$+1)OH,
∵Rt△OHB'中,OH2+B'H2=B'O2,
∴OH2+($\sqrt{2}$+1)2OH2=62,
解得OH2=18-9$\sqrt{2}$,即B′点的横坐标的平方为18-9$\sqrt{2}$;
③当FE=FB'时,如图,过点B'作B'H⊥OM于H,
∵∠EB'F=∠FEB'=45°,
∴∠EFB'=90°=∠MFO,
又∵∠OMF=45°,
∴∠MOF=45°,
∴a的度数=∠BOB'=135°,
此时,Rt△OHB'中,OH2=$\frac{1}{2}$B'O2=$\frac{1}{2}$×36=18,即B′点的横坐标的平方为18.
点评 本题属于几何变换综合题,主要考查了等腰直角三角形的性质,旋转的性质,平行线分线段成比例定理,待定系数法求函数解析式,等腰三角形的性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造直角三角形和平行线,运用分类讨论思想进行求解.解题时注意:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.

 科学实验活动册系列答案
科学实验活动册系列答案 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的有( )个.
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | $\sqrt{4}$ | B. | 3π | C. | $\frac{22}{7}$ | D. | $\root{3}{8}$ |
| A. | -0.5 | B. | 1 | C. | 2 | D. | 0.5 |
| A. | 0 | B. | ±1 | C. | 0和1 | D. | 0 或±1 |






 为响应市委市政府提出的建设“绿色泰安”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)( )
为响应市委市政府提出的建设“绿色泰安”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)( )