题目内容
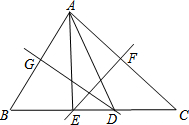如图，在△ABC中，∠BAC=72°，∠B=68度，AB、AC的垂直平分线分别交BC于D、E，则∠EAD的度数=考点：线段垂直平分线的性质
专题：
分析：由在△ABC中，∠BAC=72°，∠B=68°，根据三角形内角和定理，可求得∠C的度数，又由AB、AC的垂直平分线分别交BC于D、E，根据线段垂直平分线的性质，可求得∠BAD与∠CAE的度数，继而求得答案．
解答：解：∵在△ABC中，∠BAC=72°，∠B=68°，
∴∠C=180°-∠BAC-∠B=40°，
∵AB、AC的垂直平分线分别交BC于D、E，
∴AD=BD，AE=CE，
∴∠BAD=∠B=68°，∠EAC=∠C=40°，
∴∠EAD=∠BAD+∠CAE-∠BAC=36°．
故答案为：36．
∴∠C=180°-∠BAC-∠B=40°，
∵AB、AC的垂直平分线分别交BC于D、E，
∴AD=BD，AE=CE，
∴∠BAD=∠B=68°，∠EAC=∠C=40°，
∴∠EAD=∠BAD+∠CAE-∠BAC=36°．
故答案为：36．
点评：此题考查了线段垂直平分线的性质以及等腰三角形的性质．此题比较适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，已知AD⊥BC，若用HL判定△ABD≌△ACD，只需添加的一个条件是
如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成．若较短的直角边BC=5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图2所示的“数学风车”，若△BCD的周长是30，则这个风车的外围周长是