题目内容
11.如果(x+1)(x2-4ax+a)的乘积中不含x2项,则a为$\frac{1}{4}$.分析 先根据多项式乘以多项式法则展开,合并同类项,根据已知得出-4a+1=0,求出即可.
解答 解:(x+1)(x2-4ax+a)
=x3-4ax2+ax+x2-4ax+a
=x3+(-4a+1)x2-3ax+a,
∵(x+1)(x2-4ax+a)的乘积中不含x2项,
∴-4a+1=0,
解得:a=$\frac{1}{4}$
故答案为:$\frac{1}{4}$.
点评 本题考查了多项式乘以多项式法则和解一元一次方程,能根据多项式乘以多项式法则展开是解此题的关键.

练习册系列答案
相关题目
19.下列计算中,运算正确的是( )
| A. | (a-b)(a-b)=a2-b2 | B. | (x+2)(x-2)=x2-2 | ||
| C. | (2x+1)(2x-1)=2x2-1 | D. | (-3x+2)(-3x-2)=9x2-4 |
6.下列式子中,y是x的反比例函数的是( )
| A. | y=$\frac{1}{{x}^{2}}$ | B. | y=$\frac{x}{2}$ | C. | y=$\frac{x}{x+1}$ | D. | xy=1 |
3.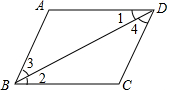 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )
 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )| A. | 因为AD∥BC,所以∠3=∠4 | B. | 因为AB∥CD,所以∠ABC+∠C=180° | ||
| C. | 因为∠1=∠2,所以AD∥BC | D. | 因为∠A+∠ADC=180°,所以AB∥CD |