题目内容
13.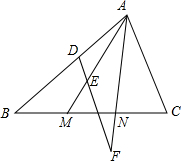 如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.
如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.
分析 过N、M分别作AC的平行线交AB于H、G,交AM于K,如图,利用平行线分线段成比例定理得到BG=GH=AH,利用三角形中位线性质得到KH=$\frac{1}{2}$GM,GM=$\frac{1}{2}$NH,则HK=$\frac{1}{4}$NH,所以$\frac{HK}{KN}$=$\frac{1}{3}$,然后利用DF∥NH得到$\frac{HK}{DE}$=$\frac{AK}{AE}$,$\frac{NK}{EF}$=$\frac{AK}{AE}$,然后利用比例性质可求出$\frac{EF}{DE}$=$\frac{1}{3}$.
解答 解: 过N、M分别作AC的平行线交AB于H、G,交AM于K,如图,
过N、M分别作AC的平行线交AB于H、G,交AM于K,如图,
∵BM=MN=NC,
∴BG=GH=AH,
∵HK∥GM,
∴KH=$\frac{1}{2}$GM,GM=$\frac{1}{2}$NH,
∴HK=$\frac{1}{4}$NH,
∴$\frac{HK}{KN}$=$\frac{1}{3}$,
∴DF∥NH,
∴$\frac{HK}{DE}$=$\frac{AK}{AE}$,$\frac{NK}{EF}$=$\frac{AK}{AE}$,
∴$\frac{HK}{DE}$=$\frac{NK}{EF}$,
∴$\frac{EF}{DE}$=$\frac{HK}{NK}$=$\frac{1}{3}$.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.作GM∥AC,NH∥AC构造平行线分线段成比例的基本图形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.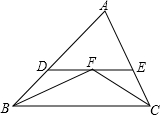 如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①∠A=2∠BFC-180°;②DE-BD=CE;③△ADE的周长等于AB与AC的和;④BF>CF.
其中正确的有( )
 如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①∠A=2∠BFC-180°;②DE-BD=CE;③△ADE的周长等于AB与AC的和;④BF>CF.
其中正确的有( )
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
2. 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )| A. | 2.5m | B. | 3m | C. | 3.5m | D. | 4m |
3.若x=-1是关于x的方程2x+m=1的解,则m-1的值是( )
| A. | 3 | B. | 2 | C. | -2 | D. | -1 |
 如图所示,设⊙O的直径为d,已知d使得关于x的方程x2+dx+2e=0和x2+2ex+d=0均有实数根(e>0),且对一切实数x,不等式|x|+|x-4|≥d均成立.若P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B、C为直线PBC与⊙O的交点,若PA、PB、PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
如图所示,设⊙O的直径为d,已知d使得关于x的方程x2+dx+2e=0和x2+2ex+d=0均有实数根(e>0),且对一切实数x,不等式|x|+|x-4|≥d均成立.若P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B、C为直线PBC与⊙O的交点,若PA、PB、PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.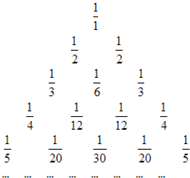 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.