题目内容
从-2,-
,
,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组
中,能使不等式组至少有两个整数解的概率是 .
| 2 |
| 3 |
| 1 |
| 2 |
|
考点:列表法与树状图法,一元一次不等式组的整数解
专题:
分析:首先解不等式组可得:
,又由-2,-
,
,1,3五个数的倒数分别为:-
,-
,2,1,
;可得将a,b代入不等式组
中,能使不等式组至少有两个整数解的是:(1,1),然后利用概率公式求解即可求得答案.
|
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
|
解答:解:解不等式组可得:
,
∵-2,-
,
,1,3五个数的倒数分别为:-
,-
,2,1,
;
∴将a,b代入不等式组
中,能使不等式组至少有两个整数解的是:(1,1),
∴将a,b代入不等式组
中,能使不等式组至少有两个整数解的概率是:
.
故答案为:
.
|
∵-2,-
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
∴将a,b代入不等式组
|
∴将a,b代入不等式组
|
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:此题考查了概率公式的应用、方程组的解法以及倒数的定义.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
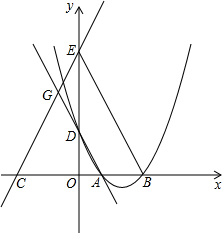 已知抛物线y=x2-(k+2)x+
已知抛物线y=x2-(k+2)x+ 如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC. 图中表示的不等式的解集是
图中表示的不等式的解集是 如图,三角板的直角顶点P在射线OM上,∠AOB=90°,OM是∠AOB的角平分线
如图,三角板的直角顶点P在射线OM上,∠AOB=90°,OM是∠AOB的角平分线