题目内容
⊙O的直径为10cm,弦AB的弦心距为3cm,则以弦AB为一边的⊙O内接矩形的周长为 cm.
考点:垂径定理,勾股定理,矩形的性质
专题:
分析:先根据题意画出图形,根据垂径定理和勾股定理求AB、AC的长度,再求周长.
解答: 解:如图,
解:如图,
∵⊙O的直径为10 cm,弦AB的弦心距为3cm,
∴连接OA,OA=5cm,
在Rt△AOG中,
∵OA=5cm,OG=3cm,
∴AG=
=
=4.
∴AB=2AG=2×4=8cm.
连接BC,则BC=10cm,
在Rt△ABC中,
∵BC=10cm,AB=8cm.
∴AC=
=
=6.
∴以弦AB为一边的⊙O内接矩形的周长为2AC+2AB=2×6+2×8=28cm.
故答案为:28..
 解:如图,
解:如图,∵⊙O的直径为10 cm,弦AB的弦心距为3cm,
∴连接OA,OA=5cm,
在Rt△AOG中,
∵OA=5cm,OG=3cm,
∴AG=
| OA2-OG2 |
| 52-32 |
∴AB=2AG=2×4=8cm.
连接BC,则BC=10cm,
在Rt△ABC中,
∵BC=10cm,AB=8cm.
∴AC=
| BC2-AB2 |
| 102-82 |
∴以弦AB为一边的⊙O内接矩形的周长为2AC+2AB=2×6+2×8=28cm.
故答案为:28..
点评:本题考查的是垂径定理,根据题意作出辅助线,利用垂径定理求解是解答此题的关键.

练习册系列答案
相关题目
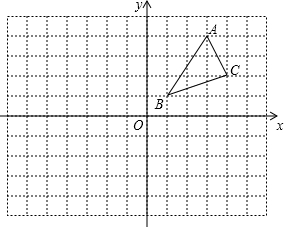 如图,点C的坐标为(4,2),作出△ABC关于y轴对称的图形△A1B1C1,再作出△A1B1C1关于原点对称的△A2B2C2,并写出点A2、B2、C2的坐标.
如图,点C的坐标为(4,2),作出△ABC关于y轴对称的图形△A1B1C1,再作出△A1B1C1关于原点对称的△A2B2C2,并写出点A2、B2、C2的坐标. 如图,小方格的边长都是1,求五边形ABCDE的周长和面积?
如图,小方格的边长都是1,求五边形ABCDE的周长和面积?
 如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,视为无效,重新转动一次转盘),此过程称为一次操作.
如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,视为无效,重新转动一次转盘),此过程称为一次操作.