题目内容
11.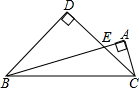 如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.
如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.
分析 过E作EF⊥BC,交BC于点F,在直角三角形BDC中,由BC的长求出DB与DC的长,由三角形DCB为等腰直角三角形,由∠DBC-∠ABC求出∠DBA的度数,在直角三角形BDE中,设DE=x,利用30度角所对的直角边等于斜边的一半得到BE=2x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出DC的长,由DC-DE求出EC的长,在等腰直角三角形ECF中,求出EF的长,由BC为底边,EF为高,求出三角形BEC面积即可.
解答 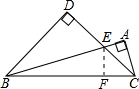 解:过E作EF⊥BC,交BC于点F,
解:过E作EF⊥BC,交BC于点F,
在Rt△BDC中,BC=2$\sqrt{3}$,
根据勾股定理得:DB=DC=$\frac{\sqrt{2}}{2}$BC=$\sqrt{6}$,
∵△DCB为等腰直角三角形,∠ABC=15°,
∴∠DBA=∠DBC-∠ABC=45°-15°=30°,
在Rt△BED中,BD=$\sqrt{6}$,∠DBE=30°,
设DE=x,则有BE=2x,
根据勾股定理得:BE2=BD2+DE2,即4x2=6+x2,
解得:x=$\sqrt{2}$,
∴EC=DC-DE=$\sqrt{6}$-$\sqrt{2}$,
∵△EFC为等腰直角三角形,
∴EF=FC=$\frac{\sqrt{2}}{2}$×($\sqrt{6}$-$\sqrt{2}$)=$\sqrt{3}$-1,
则S△BEC=$\frac{1}{2}$BC•EF=3-$\sqrt{3}$.
故答案为:3-$\sqrt{3}$
点评 此题考查了勾股定理,含30度直角三角形的性质,等腰直角三角形的性质,以及三角形面积求法,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.本学年的五次数学测试中,甲、乙两同学的平均成绩一样,方差分别为0.5,1.2,则下列说法正确的是( )
| A. | 甲、乙两位同学的成绩一样稳定 | B. | 甲同学的成绩更稳定 | ||
| C. | 乙同学的成绩更稳定 | D. | 两位同学的成绩的稳定性不能确定 |