题目内容
2.某汽车销售公司10月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为18万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在8部以内(含8部),每部返利0.5万元;销售量在8部以上,每部返利1万元.(1)若该公司当月售出4部汽车,则每部汽车的进价为17.7万元;
(2)如果汽车的售价为19万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
分析 (1)根据若当月仅售出1部汽车,则该部汽车的进价为18万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,得出该公司当月售出3部汽车时,则每部汽车的进价为:15-0.1×3,即可得出答案;
(2)利用设需要售出x部汽车,由题意可知,每部汽车的销售利润,根据当0≤x≤8,以及当x>8时,分别讨论得出即可
解答 解:(1)∵若当月仅售出1部汽车,则该部汽车的进价为18万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,
∴若该公司当月售出4部汽车,则每部汽车的进价为:18-0.1×3=17.7,
故答案为:17.7;
(2)设需要售出x部汽车,由题意可知,每部汽车的销售利润为:
19-[18-0.1(x-1)]=(0.1x+0.9)(万元),
当0≤x≤8,
根据题意,得x•(0.1x+0.9)+0.5x=12,
整理,得x2+14x-120=0,
解这个方程,得x1=-20(不合题意,舍去),x2=6,
当x>8时,
根据题意,得x•(0.1x+0.9)+x=12,
整理,得x2+19x-120=0,
解这个方程,得x1=-24(不合题意,舍去),x2=5,
因为5<8,所以x2=5舍去,
答:需要售出6部汽车.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系并进行分段讨论是解题关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
13. 如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
 如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )| A. | 22° | B. | 28° | C. | 32° | D. | 38° |
17.据四川新闻网3月3日报道,成都地铁春运至今(2013年3月3日止),成都地铁运送乘客21600000人次,用科学记数法表示为( )
| A. | 2.16×108人 | B. | 2.16×107人 | C. | 0.216×108人 | D. | 216×105人 |
7.如图是我国几家银行的标志,在这几个图形中是轴对称图形的有( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
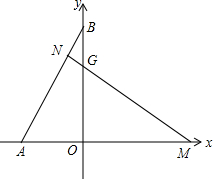 在平面直角坐标中,x轴上有点A和点M,y轴上有一点B,过点M作MN⊥AB于点N,交y轴于点G,且MG=AB,OA、OM(OA<OM)的长是方程x2-7x+12=0的两个根.
在平面直角坐标中,x轴上有点A和点M,y轴上有一点B,过点M作MN⊥AB于点N,交y轴于点G,且MG=AB,OA、OM(OA<OM)的长是方程x2-7x+12=0的两个根.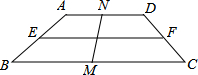 如图,在梯形ABCD中AD∥BC,∠B=40°,∠C=50°,E、M、F、N分别是边AB、BC、CD、DA的中点,且EF=a,MN=b,则BC的长为a+b.
如图,在梯形ABCD中AD∥BC,∠B=40°,∠C=50°,E、M、F、N分别是边AB、BC、CD、DA的中点,且EF=a,MN=b,则BC的长为a+b.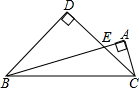 如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.
如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.