题目内容
 23、如图,下列三个论断:(1)AE∥BC,(2)AE平分∠DAC,(3)∠B=∠C,以其中两个为条件,另一个为结论,写出一个正确的命题,并说明理由.
23、如图,下列三个论断:(1)AE∥BC,(2)AE平分∠DAC,(3)∠B=∠C,以其中两个为条件,另一个为结论,写出一个正确的命题,并说明理由.条件是
(1)(2)
结论是(3)
.分析:由(1)AE∥BC得到∠DAE=∠B,∠EAC=∠C;由(2)AE平分∠DAC得到∠DAE=∠EAC,从而得到结论.在这三个论断中只要已知其中的两个,就可以得出另外的一个.
解答:解:例如:已知AE∥BC,AE平分∠DAC,求证∠B=∠C.
证明:∵AE∥BC,
∴∠DAE=∠B(两直线平行,同位角相等),
∴∠EAC=∠C(两直线平行,内错角相等),
∵AE平分∠DAC,
∴∠DAE=∠EAC,
∴∠B=∠C(等量代换).
证明:∵AE∥BC,
∴∠DAE=∠B(两直线平行,同位角相等),
∴∠EAC=∠C(两直线平行,内错角相等),
∵AE平分∠DAC,
∴∠DAE=∠EAC,
∴∠B=∠C(等量代换).
点评:这是一个开放性问题,答案不唯一,是中考中经常出现的一个题型.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
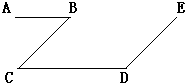 21、如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏中,使之成为一道由已知可得到结论的题目,并说明理由.
21、如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏中,使之成为一道由已知可得到结论的题目,并说明理由. 22、如图,BC与DE相交于O点,给出下列三个论断:①∠B=∠E,②AB∥DE,③BC∥EF.
22、如图,BC与DE相交于O点,给出下列三个论断:①∠B=∠E,②AB∥DE,③BC∥EF. 如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏”中,使之成为一道由已知可得到结论的题目,并说明理由
如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏”中,使之成为一道由已知可得到结论的题目,并说明理由 如图,下列三个论断:(1)AE∥BC,(2)AE平分∠DAC,(3)∠B=∠C,以其中两个为条件,另一个为结论,写出一个正确的命题,并说明理由.
如图,下列三个论断:(1)AE∥BC,(2)AE平分∠DAC,(3)∠B=∠C,以其中两个为条件,另一个为结论,写出一个正确的命题,并说明理由.