Question

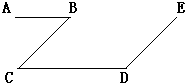21、如图，给出下列三个论断：①∠B+∠D=180°；②AB∥CD；③BC∥DE．请你以其中两个论断作为已知条件，填入“已知”栏中，以一个论断作为结论，填入“结论栏中，使之成为一道由已知可得到结论的题目，并说明理由．
已知，如图，

①②

，
结论：

③

．
理由：

平行线的判定与性质

．

Answer 1

分析：①、②可得到③．由于AB∥CD，易知∠B=∠C，而∠B+∠D=180°，那么∠C+∠D=180°，从而可证BC∥DE．

解答：解：如果∠B+∠D=180°，AB∥CD，那么BC∥DE．理由如下：
∵AB∥CD（已知），
∴∠B=∠C（两直线平行，内错角相等），
又∵∠B+∠D=180°（已知），
∴∠C+∠D=180°，
∴BC∥DE（同旁内角互补，两直线平行）．
故答案是①②，③，平行线的判定与性质．

点评：本题考查了平行线的判定和性质，解题的关键是灵活掌握平行线的判定和性质．