题目内容
 如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏”中,使之成为一道由已知可得到结论的题目,并说明理由
如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏”中,使之成为一道由已知可得到结论的题目,并说明理由已知,如图,
①②
①②
,结论:
③
③
.理由:
∵AB∥CD,
∴∠B=∠BCD,
∵∠B+∠D=180°,
∴∠BCD+∠D=180°,
∴BC∥DE.
∴∠B=∠BCD,
∵∠B+∠D=180°,
∴∠BCD+∠D=180°,
∴BC∥DE.
∵AB∥CD,
∴∠B=∠BCD,
∵∠B+∠D=180°,
∴∠BCD+∠D=180°,
∴BC∥DE.
.∴∠B=∠BCD,
∵∠B+∠D=180°,
∴∠BCD+∠D=180°,
∴BC∥DE.
分析:根据平行线性质得出∠B=∠BCD,推出∠BCD+∠D=180°,根据平行线的判定推出即可,此题也可以由②③推出①,或由①③推出②.
解答:解:理由是:∵AB∥CD,
∴∠B=∠BCD,
∵∠B+∠D=180°,
∴∠BCD+∠D=180°,
∴BC∥DE,
故答案为:①②,③,∵AB∥CD,∴∠B=∠BCD,∵∠B+∠D=180°,∴∠BCD+∠D=180°,∴BC∥DE.
∴∠B=∠BCD,
∵∠B+∠D=180°,
∴∠BCD+∠D=180°,
∴BC∥DE,
故答案为:①②,③,∵AB∥CD,∴∠B=∠BCD,∵∠B+∠D=180°,∴∠BCD+∠D=180°,∴BC∥DE.
点评:本题考查了平行线性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
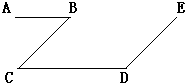 21、如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏中,使之成为一道由已知可得到结论的题目,并说明理由.
21、如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏中,使之成为一道由已知可得到结论的题目,并说明理由. 如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏”中,使之成为一道由已知可得到结论的题目,并说明理由
如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏”中,使之成为一道由已知可得到结论的题目,并说明理由
