题目内容
5.已知代数式$\sqrt{1-x}$+$\sqrt{\frac{1}{x}}$在实数范围内有意义,则x的取值范围是( )| A. | 0<x≤1 | B. | x≥1 | C. | x>0 | D. | 0≤x≤1 |
分析 根据二次根式有意义的条件,可得结果.
解答 解:∵代数式$\sqrt{1-x}$+$\sqrt{\frac{1}{x}}$在实数范围内有意义,
∴1-x≥0,x>0,
∴0<x≤1,
故选A.
点评 本题主要考查了二次根式有意义的条件,注意x≠0是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列分式是最简分式的( )
| A. | $\frac{a+b}{{{a^2}+{b^2}}}$ | B. | $\frac{a}{{{a^2}-3a}}$ | C. | $\frac{2a}{{3{a^2}b}}$ | D. | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |
20.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{{x}^{2}}$ | B. | $\frac{x}{\sqrt{3}}$ | C. | $\sqrt{8}$ | D. | $\frac{\sqrt{2x}}{2}$ |
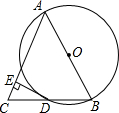 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为E.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为E. 在2011元旦化妆晚会上,学生小明自制了一个无底圆锥形纸帽,如图所示,围成这个纸帽的面积是48πcm2.
在2011元旦化妆晚会上,学生小明自制了一个无底圆锥形纸帽,如图所示,围成这个纸帽的面积是48πcm2. 如图,一次函数y=kx+b(k<0)的图象过点(0,-2),则不等式kx+b<-2的解集是x>0.
如图,一次函数y=kx+b(k<0)的图象过点(0,-2),则不等式kx+b<-2的解集是x>0.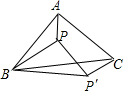 如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.
如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.