题目内容
20. △ABC在如图的直角坐标系中,
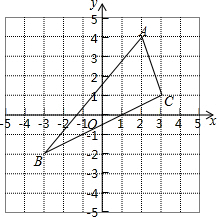
△ABC在如图的直角坐标系中,(1)写出点A,B,C的坐标:A:(2,4),B:(-3,-2),C:(3,1).
(2)写出△ABC中点A,B,C关于y轴对称的△A′B′C′的对称点A′,B′,C′的坐标分别是A′:(-2,4),B′:(3,-2),C′:(-3,1).
(3)求出△ABC的面积.
分析 (1)根据点的位置,可得点的坐标;
(2)根据关于y轴对称的点的横坐标互为相反数,纵坐标相等,可得答案;
(3)根据图形割补法,可得规则的图形,根据面积的和差,可得答案.
解答 解:(1)写出点A,B,C的坐标:A:(2,4),B:(-3,-2),C:(3,1).
(2)写出△ABC中点A,B,C关于y轴对称的△A′B′C′的对称点A′,B′,C′的坐标分别是A′:(-2,4),B′:(3,-2),C′:(-3,1);
故答案为:(2,4),(-3,-2),(3,1);(-2,4),(3,-2),(-3,1);
(3)如图:
S△ABC=S正方形BDEF-S△BCD-S△ACE-S△ABF=6×6-$\frac{1}{2}$×6×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×5×6=$\frac{21}{2}$.
点评 本题考查了关于y轴对称的点的坐标,关于y轴对称的点的横坐标互为相反数,纵坐标相等,利用图形割补法是求面积的关键.

练习册系列答案
相关题目
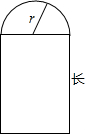 一个窗框的形状如图所示,已知窗框外围的周长为l,半圆的半径为r.
一个窗框的形状如图所示,已知窗框外围的周长为l,半圆的半径为r.