题目内容
6.用配方法解方程x2+4x-4=0,配方变形结果正确的是( )| A. | (x+2)2=-8 | B. | (x-2)2=-8 | C. | (x-2)2=8 | D. | (x+2)2=8 |
分析 在本题中,把常数项-4移项后,应该在左右两边同时加上一次项系数4的一半的平方.
解答 解:把方程x2+4x-4=0的常数项移到等号的右边,得到x2+4x=4,
方程两边同时加上一次项系数一半的平方,得到x2+4x+22=4+22,
配方得(x+2)2=8.
故选:D.
点评 本题考查了解一元二次方程--配方法.配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如图,在平面直角坐标系中,一动点从原点O出发,向上,向右,向下,向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A42的坐标为 ( )


| A. | (20,0) | B. | (20,1) | C. | (21,0) | D. | (21,1) |
17. 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.在平面直角坐标系xOy中,如果⊙O是以原点O(0,0)为圆心,以5为半径的圆,那么点A(-3,-4)与⊙O的位置关系是( )
| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
11.某样本容量是60,分组后,第2组的频率是0.15,那么第2组的频数是( )
| A. | 9 | B. | 18 | C. | 60 | D. | 400 |
15.化简$\sqrt{18}$÷$\sqrt{2}$的结果是( )
| A. | 9 | B. | 3 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
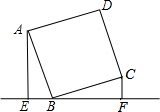 如图,直线L过正方形ABCD的顶点B,点A、点C到直线L的距离分别是2和1,求正方形ABCD的边长?
如图,直线L过正方形ABCD的顶点B,点A、点C到直线L的距离分别是2和1,求正方形ABCD的边长?


