题目内容
13.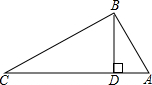 如图所示,三个村庄A,B,C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC.已知公路的造价为25000元/km,求修条公路的最低造价是多少元?
如图所示,三个村庄A,B,C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC.已知公路的造价为25000元/km,求修条公路的最低造价是多少元?
分析 首先得出BC2+AB2=122+52=169,AC2=132=169,然后利用其逆定理得到∠ABC=90°确定最短距离,然后利用面积相等求得BD的长,最终求得最低造价.
解答 解:∵BC2+AB2=122+52=169,
AC2=132=169,
∴BC2+AB2=AC2,
∴∠ABC=90°,
当BD⊥AC时BD最短,造价最低,
∵S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BD,
∴BD=$\frac{AB•CB}{AC}$=$\frac{60}{13}$km,
$\frac{60}{13}$×25000=$\frac{1500000}{13}$元.
答:最低造价为$\frac{1500000}{13}$元.
点评 本题考查了勾股定理的应用,利用垂线段最短得出当BD⊥AC时BD最短,造价最低,再利用三角形面积求出是解题关键.

练习册系列答案
相关题目
3.下列句子中,是命题的是( )
| A. | 三角两边之和大于第三边吗? | B. | 作线段AB∥CD | ||
| C. | 连结A、B两点 | D. | 正数大于负数 |
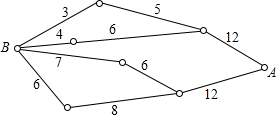 如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为( )
如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为( ) 如图,AB∥CD,∠1=64°,FG平分∠EFC,则∠EGF=64°°.
如图,AB∥CD,∠1=64°,FG平分∠EFC,则∠EGF=64°°.