题目内容
如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=- x2+bx+c经过A、C两点,与AB边交于点D.
x2+bx+c经过A、C两点,与AB边交于点D.(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线y=-
 x2+bx+c的对称轴l上若存在点F,使△FDQ为直角三角形?若存在,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上若存在点F,使△FDQ为直角三角形?若存在,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
【答案】分析:(1)将A、C两点坐标代入抛物线y=- x2+bx+c,即可求得抛物线的解析式;
x2+bx+c,即可求得抛物线的解析式;
(2)①先用m 表示出QE的长度,进而求出三角形的面积S关于m的函数,化简为顶点式,便可求出S的最大值;
②直接写出满足条件的F点的坐标即可,注意不要漏写.
解答:解:(1)将A、C两点坐标代入抛物线y=- x2+bx+c,
x2+bx+c,
 ,
,
解得 ,
,
∴抛物线的解析式为y=- x2+
x2+ x+8;
x+8;
(2)①∵OA=8,OC=6
∴AC= =10,
=10,
过点Q作QE⊥BC与E点,则sin∠ACB= =
= =
= ,
,
∴ =
= ,
,
∴QE= (10-m),
(10-m),
∴S= •CP•QE=
•CP•QE= m×
m× (10-m)=-
(10-m)=- m2+3m=-
m2+3m=- (m-5)2+
(m-5)2+ ,
,
∴当m=5时,S取最大值;
②在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=- x2+
x2+ x+8的对称轴为x=
x+8的对称轴为x= ,
,
D的坐标为(3,8),Q(3,4),
当∠FDQ=90°时,F1( ,8),
,8),
当∠FQD=90°时,则F2( ,4),
,4),
当∠DFQ=90°时,设F( ,n),
,n),
则FD2+FQ2=DQ2,
即 +(8-n)2+
+(8-n)2+ +(n-4)2=16,
+(n-4)2=16,
解得:n=6± ,
,
∴F3( ,6+
,6+ ),F4(
),F4( ,6-
,6- ),
),
满足条件的点F共有四个,坐标分别为
F1( ,8),F2(
,8),F2( ,4),F3(
,4),F3( ,6+
,6+ ),F4(
),F4( ,6-
,6- ).
).
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法抛物线的最值等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.
 x2+bx+c,即可求得抛物线的解析式;
x2+bx+c,即可求得抛物线的解析式;(2)①先用m 表示出QE的长度,进而求出三角形的面积S关于m的函数,化简为顶点式,便可求出S的最大值;
②直接写出满足条件的F点的坐标即可,注意不要漏写.
解答:解:(1)将A、C两点坐标代入抛物线y=-
 x2+bx+c,
x2+bx+c, ,
,解得
 ,
,∴抛物线的解析式为y=-
 x2+
x2+ x+8;
x+8;(2)①∵OA=8,OC=6

∴AC=
 =10,
=10,过点Q作QE⊥BC与E点,则sin∠ACB=
 =
= =
= ,
,∴
 =
= ,
,∴QE=
 (10-m),
(10-m),∴S=
 •CP•QE=
•CP•QE= m×
m× (10-m)=-
(10-m)=- m2+3m=-
m2+3m=- (m-5)2+
(m-5)2+ ,
,∴当m=5时,S取最大值;
②在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=-
 x2+
x2+ x+8的对称轴为x=
x+8的对称轴为x= ,
,D的坐标为(3,8),Q(3,4),
当∠FDQ=90°时,F1(
 ,8),
,8),当∠FQD=90°时,则F2(
 ,4),
,4),当∠DFQ=90°时,设F(
 ,n),
,n),则FD2+FQ2=DQ2,
即
 +(8-n)2+
+(8-n)2+ +(n-4)2=16,
+(n-4)2=16,解得:n=6±
 ,
,∴F3(
 ,6+
,6+ ),F4(
),F4( ,6-
,6- ),
),满足条件的点F共有四个,坐标分别为
F1(
 ,8),F2(
,8),F2( ,4),F3(
,4),F3( ,6+
,6+ ),F4(
),F4( ,6-
,6- ).
).点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法抛物线的最值等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
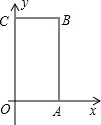 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5). 17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为
17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为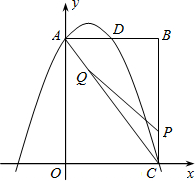

 如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )
如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )