题目内容
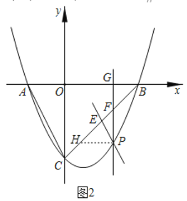
【题目】已知![]() ABC内接于
ABC内接于![]() ,
,![]() 的平分线交
的平分线交![]() 于点D,连接DB,DC.
于点D,连接DB,DC.
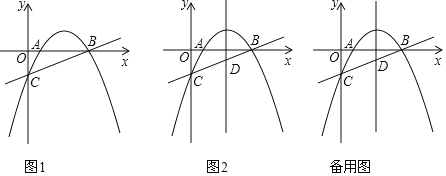
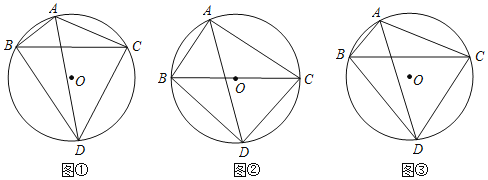
(1)如图①,当![]() 时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
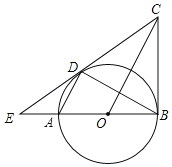
(2)如图②,当![]() 时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
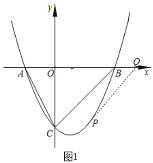
(3)如图③,若BC=5,BD=4,求![]() 的值.
的值.
【答案】(1)AB+AC=AD;(2)![]() ;(3)
;(3)![]()
【解析】
(1)在AD上截取AE=AB,连接BE,由条件可知△ABE和△BCD都是等边三角形,可证明△BED≌△BAC,可得DE=AC,则AB+AC=AD;
(2)延长AB至点M,使BM=AC,连接DM,证明△MBD≌△ACD,可得MD=AD,证得AB+AC=![]() ;
;
(3)延长AB至点N,使BN=AC,连接DN,证明△NBD≌△ACD,可得ND=AD,∠N=∠CAD,证△NAD∽△CBD,可得![]() ,
,
可由AN=AB+AC,求出![]() 的值.
的值.
解:(1)如图①在AD上截取AE=AB,连接BE,
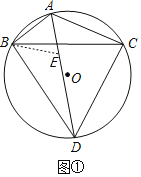
∵∠BAC=120°,∠BAC的平分线交⊙O于点D,
∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,
∴△ABE和△BCD都是等边三角形,
∴∠DBE=∠ABC,AB=BE,BC=BD,
∴△BED≌△BAC(SAS),
∴DE=AC,
∴AD=AE+DE=AB+AC;
故答案为:AB+AC=AD.
(2)AB+AC=![]() .理由如下:
.理由如下:
如图②,延长AB至点M,使BM=AC,连接DM,
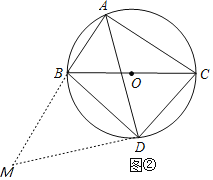
∵四边形ABDC内接于⊙O,
∴∠MBD=∠ACD,
∵∠BAD=∠CAD=45°,
∴BD=CD,
∴△MBD≌△ACD(SAS),
∴MD=AD,∠M=∠CAD=45°,
∴MD⊥AD.
∴AM=![]() ,即AB+BM=
,即AB+BM=![]() ,
,
∴AB+AC=![]() ;
;
(3)如图③,延长AB至点N,使BN=AC,连接DN,
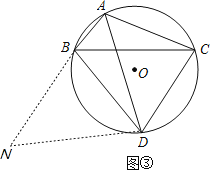
∵四边形ABDC内接于⊙O,
∴∠NBD=∠ACD,
∵∠BAD=∠CAD,
∴BD=CD,
∴△NBD≌△ACD(SAS),
∴ND=AD,∠N=∠CAD,
∴∠N=∠NAD=∠DBC=∠DCB,
∴△NAD∽△CBD,
∴![]() ,
,
∴![]() ,
,
又AN=AB+BN=AB+AC,BC=5,BD=4,
∴![]() .
.