题目内容
如图,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB = 8cm,BC = 10 cm,求EC的长
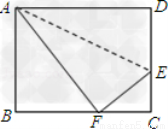
CE=3cm
【解析】
试题分析:要求CE的长,应先设CE的长为x,由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AEF,所以AF=10cm,EF=DE=8-x;在Rt△ABF中由勾股定理得:AB2+BF2=AF2,已知AB、AF的长可求出BF的长,又CF=BC-BF=10-BF,在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即:(8-x)2=x2+(10-BF)2,将求出的BF的值代入该方程求出x的值,即求出了CE的长.
试题解析:根据题意得:Rt△ADE≌Rt△AEF,
∴∠AFE=90°,AF=10cm,EF=DE,
设CE=xcm,则DE=EF=CD-CE=8-x,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC-BF=10-6=4(cm),
在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,
即(8-x)2=x2+42,
∴64-16x+x2=x2+16,
∴x=3(cm),
即CE=3cm.
考点:1.勾股定理;2.翻折变换(折叠问题).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与
与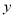 轴交于点C,与
轴交于点C,与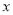 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
 的对称轴是直线x=1
的对称轴是直线x=1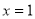 ,且图像经过点
,且图像经过点 (3,0),则
(3,0),则 的值为( )
的值为( )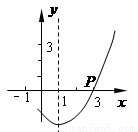
 ③;(2)①③
③;(2)①③ ②;(3)②③
②;(3)②③
 ,则实际时间是
,则实际时间是 