Question

9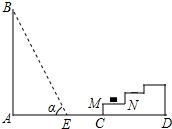．如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC=17.2米，设太阳光线与水平地面的夹角为α，当α=60°时，测得楼房在地面上的影长AE=10米，现有一只小猫睡在台阶的MN这层上晒太阳．（$\sqrt{3}$取1.73）
（1）求楼房的高度约为多少米？
（2）过了一会儿，当α=45°时，问小猫能否还晒到太阳？请说明理由．

Answer 1

分析 （1）在Rt△ABE中，由tan60°=$\frac{AB}{AE}$=$\frac{AB}{10}$，即可求出AB=10•tan60°=17.3米；
（2）假设没有台阶，当α=45°时，从点B射下的光线与地面AD的交点为点F，与MC的交点为点H．由∠BFA=45°，可得AF=AB=17.3米，那么CF=AF-AC=0.1米，CH=CF=0.1米，所以大楼的影子落在台阶MC这个侧面上，故小猫仍可以晒到太阳．

解答 解：（1）当α=60°时，在Rt△ABE中，
∵tan60°=$\frac{AB}{AE}$=$\frac{AB}{10}$，
∴AB=10•tan60°=10$\sqrt{3}$≈10×1.73=17.3米．
即楼房的高度约为17.3米；

（2）当α=45°时，小猫仍可以晒到太阳．理由如下：
假设没有台阶，当α=45°时，从点B射下的光线与地面AD的交点为点F，与MC的交点为点H．
∵∠BFA=45°，
∴tan45°=$\frac{AB}{AF}$=1，
此时的影长AF=AB=17.3米，
∴CF=AF-AC=17.3-17.2=0.1米，
∴CH=CF=0.1米，
∴大楼的影子落在台阶MC这个侧面上，
∴小猫仍可以晒到太阳．

点评 本题考查了解直角三角形的应用，锐角三角函数定义，理解题意，将实际问题转化为数学问题是解题的关键．