题目内容
17.已知△ABC的三边长为a,b,c,化简$\sqrt{(a+b+c)^{2}}$+$\sqrt{(a-b-c)^{2}}$-$\sqrt{(c-a-b)^{2}}$.分析 根据三角形三边关系即可判断a+b+c、a-b-c、c-a-b与0的大小关系,从而根据二次根式的性质即可求出答案.
解答 解:∵a,b,c为△ABC的三边长,
∴a+b+c>0,b+c>a,a+b>c,
∴a-b-c<0,c-a-b<0
∴$\sqrt{{{({a+b+c})}^2}}+\sqrt{{{({a-b-c})}^2}}-\sqrt{{{({c-a-b})}^2}}$
=|a+b+c|+|a-b-c|-|c-a-b|
=a+b+c-(a-b-c)+(c-a-b)
=a+b+c+b+c-a+c-a-b
=-a+b+3c
点评 本题考查二次根式的性质,解题的关键是根据三角形的三边关系进行化简,本题属于中等题型.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
14.要对大批量生产的商品进行检验,下列做法比较合适的是( )
| A. | 把所有商品逐渐进行检验 | |
| B. | 从中抽取1件进行检验 | |
| C. | 从中挑选几件进行检验 | |
| D. | 从中按抽样规则抽取一定数量的商品进行检验 |
12.减去3x2-4x+1等于3x2-2x-1的多项式为( )
| A. | 6x2-6x | B. | 2x-1 | C. | 6x2+6x-2 | D. | 6x2+6x+2 |
9.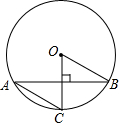 如图,AB是⊙O的弦,半径OC⊥AB,AC∥OB,则∠BOC的度数为( )
如图,AB是⊙O的弦,半径OC⊥AB,AC∥OB,则∠BOC的度数为( )
 如图,AB是⊙O的弦,半径OC⊥AB,AC∥OB,则∠BOC的度数为( )
如图,AB是⊙O的弦,半径OC⊥AB,AC∥OB,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
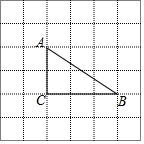 如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则△ABC的周长是8.606单位长度(精确到0.001)
如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则△ABC的周长是8.606单位长度(精确到0.001)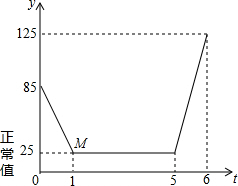 近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题:
近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题: 如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO=$\sqrt{2}$BE,则线段OD=2$\sqrt{7}$,BE=4.
如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO=$\sqrt{2}$BE,则线段OD=2$\sqrt{7}$,BE=4.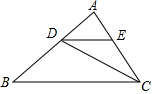
 如图,△ABC中,M是BC中点,AD平分∠BAC,BD⊥AD于D,若AB=12,AC=16,则MD等于2.
如图,△ABC中,M是BC中点,AD平分∠BAC,BD⊥AD于D,若AB=12,AC=16,则MD等于2.