Question

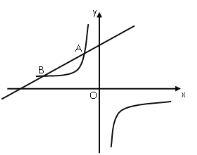
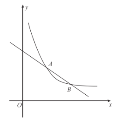
【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数（）的图象交于，两点．

（1）求的值；

（2）求出一次函数与反比例函数的表达式；

（3）过点作轴的垂线，与直线和函数（）的图象的交点分别为点，，当点在点下方时，写出的取值范围．

Answer 1

【答案】（1）；（2），（）；（3）或．

【解析】

（1）根据 可求m；

（2）根据（1）中m的值求出A和B点坐标，运用待定系数法即可求一次函数和反比例函数解析式；

（3）观察图象，以A，B点作为分界点，利用数形结合的思想求解．

解：（1）由反比例函数概念可得，解得．

（2）∵m=3，

∴，，

将点，代入得解得

所以一次函数的解析式为．

由，可得反比例函数的解析式为（）．

（3）∵两函数的交点坐标是A（3，4），B（6，2），
∴当点M在点N下方时，a的取值范围是0＜a＜3或a＞6．