题目内容
某商场服装部销售一种名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售.经调查,每件降价1元时,平均每天可多卖出2件.
(1)若商场要求该服装部每天盈利1200元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多?
(1)若商场要求该服装部每天盈利1200元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多?
考点:二次函数的应用
专题:
分析:(1)利用每件衬衫每降价1元,商场平均每天可多售出2件,即可得出每件衬衣降价x元,每天可以多销售2x件,进而得出y与x的函数关系式;
再利用商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),把相关数值代入即可求解;
(2)利用商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),利用二次函数最值求法得出即可.
再利用商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),把相关数值代入即可求解;
(2)利用商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),利用二次函数最值求法得出即可.
解答:解:(1)∵某商场销售一批品牌衬衫,平均每天可售出20件,如果每件衬衫每降价1元,商场平均每天可多售出2件.
∴每件衬衣降价x元,每天可以销售y件,y与x的函数关系式为:y=20+2x;
∵商场平均每天要盈利1200元,
∴(40-x)(20+2x)=1200,
整理得:2x2-60x+400=0,
解得:x1=20,x2=10,
因为要减少库存,在获利相同的情况下,降价越多,销售越快,故每件衬衫应降20元;
(2)设商场平均每天赢利w元,
则 w=(20+2x)(40-x),
=-2x2+60x+800,
=-2(x-15)2+1250.
∴当x=15时,w取最大值,最大值为1250.
答:每件衬衫降价15元时,商场平均每天赢利最多,最大利润为1250元.
∴每件衬衣降价x元,每天可以销售y件,y与x的函数关系式为:y=20+2x;
∵商场平均每天要盈利1200元,
∴(40-x)(20+2x)=1200,
整理得:2x2-60x+400=0,
解得:x1=20,x2=10,
因为要减少库存,在获利相同的情况下,降价越多,销售越快,故每件衬衫应降20元;
(2)设商场平均每天赢利w元,
则 w=(20+2x)(40-x),
=-2x2+60x+800,
=-2(x-15)2+1250.
∴当x=15时,w取最大值,最大值为1250.
答:每件衬衫降价15元时,商场平均每天赢利最多,最大利润为1250元.
点评:此题主要考查了一元二次方程的应用以及二次函数的应用,解决本题的关键是找到销售利润的等量关系,难点是得到降价后增加的销售量.

练习册系列答案
相关题目
-7-5等于( )
| A、-2 | B、2 | C、-12 | D、12 |
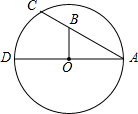 如图,AD是⊙O的直径,AC为弦,∠CAD=30°,OB⊥AD于O,交AC于B,AB=5,求BC的长.
如图,AD是⊙O的直径,AC为弦,∠CAD=30°,OB⊥AD于O,交AC于B,AB=5,求BC的长.