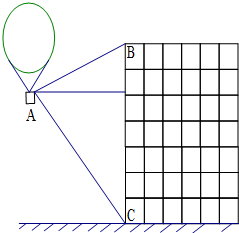
题目内容
 热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A处与高楼的水平距离为60m,这栋高楼有多高?(结果精确到0.1m,参考数据:
热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A处与高楼的水平距离为60m,这栋高楼有多高?(结果精确到0.1m,参考数据:| 2 |
| 3 |
分析:过A作AD⊥BC于D.在Rt△ADC和Rt△ABD中,运用三角函数定义求解.
解答: 解:过点A作BC的垂线,垂足为D点. (1分)
解:过点A作BC的垂线,垂足为D点. (1分)
由题意知:∠CAD=45°,∠BAD=60°,AD=60.
在Rt△ACD中,∠CAD=45°,AD⊥BC,
∴CD=AD=60. (3分)
在Rt△ABD中,
∵tan∠BAD=
,(4分)
∴BD=AD•tan∠BAD
=60
. (5分)
∴BC=CD+BD
=60+60
(6分)
≈163.9(m). (7分)
答:这栋高楼约有163.9m. (8分)
(本题其它解法参照此标准给分)
 解:过点A作BC的垂线,垂足为D点. (1分)
解:过点A作BC的垂线,垂足为D点. (1分)由题意知:∠CAD=45°,∠BAD=60°,AD=60.
在Rt△ACD中,∠CAD=45°,AD⊥BC,
∴CD=AD=60. (3分)
在Rt△ABD中,
∵tan∠BAD=
| BD |
| AD |
∴BD=AD•tan∠BAD
=60
| 3 |
∴BC=CD+BD
=60+60
| 3 |
≈163.9(m). (7分)
答:这栋高楼约有163.9m. (8分)
(本题其它解法参照此标准给分)
点评:本题考查仰角俯角的定义,要求学生能借助仰角俯角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
 21、热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为28°,看这栋高楼底部的俯角为62°,热气球与高楼之间的水平距离为66m,这栋高楼有多高?(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
21、热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为28°,看这栋高楼底部的俯角为62°,热气球与高楼之间的水平距离为66m,这栋高楼有多高?(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88) 如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°.热气球A的高度为240米,求这栋大楼的高度.
如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°.热气球A的高度为240米,求这栋大楼的高度.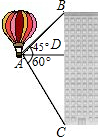 如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(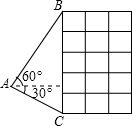 如图热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为60°,看这栋高楼底部的俯角为30°,若热气球与高楼水平距离为60m,则这栋楼的高度为
如图热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为60°,看这栋高楼底部的俯角为30°,若热气球与高楼水平距离为60m,则这栋楼的高度为 (2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
(2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )