题目内容
4.已知抛物线y=-x2+2x+8.(1)求它与x轴的交点和抛物线顶点的坐标.
(2)x取什么值时,抛物线在x轴上方?x取什么值时,y的值随x的值的增大而减小.
分析 (1)令y=0,即可求得它与x轴的交点,再由抛物线的顶点坐标求得答案即可;
(2)根据抛物线和x轴的交点坐标,再由抛物线的开口向下,即可得出x的取值范围;根据抛物线的性质,抛物线开口向下,在对称轴的左侧,y的值随x值的增大而减小,即可得出x的取值范围.
解答 (1)令y=0,得-x2+2x+8=0,解得x1=4,x2=-2,
∴与 x 轴的交点坐标是(-2,0)( 4,0),
∵y=-x2+2x+8=-(x-1)2+9,
∴顶点的坐标( 1,9);
( 2)∵抛物线的开口向下,
∴当-2<x<4时,抛物线在x轴上方.
∵抛物线的开口向下,对称轴x=1,
∴x>1,y的值随 x 值的增大而减小.
点评 本题考查了抛物线与x轴的交点问题,二次函数的性质以及待定系数法求二次函数的解析式,熟练掌握二次函数的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.二次函数y=a(x-m)2+2m,无论m为何实数,其图象的顶点必在( )
| A. | 直线y=-2x上 | B. | x轴上 | C. | y轴上 | D. | 直线y=2x上 |
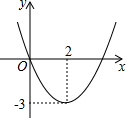 某同学从图中(二次函数y=ax2+bx+c)观察得出下面五条信息①a<0,②c=0,③函数的最小值为-3,④当x<0时,y>0,⑤函数的对称轴为x=2,你认为其中正确的有:②③④⑤(填出序号)
某同学从图中(二次函数y=ax2+bx+c)观察得出下面五条信息①a<0,②c=0,③函数的最小值为-3,④当x<0时,y>0,⑤函数的对称轴为x=2,你认为其中正确的有:②③④⑤(填出序号) 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.