题目内容
【题目】如图，菱形ABCD的顶点A在反比例函数
的图象上，B（0，-5）、D在
轴上，点E（-4，0）是
与x轴的交点，若菱形ABCD面积
，则k值为（ ）
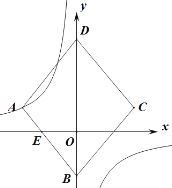
A.-36B.-16C.
D.-24
【答案】C
【解析】
由题意设A（m，n），根据菱形的面积公式进行分析并作AF⊥x轴于F，进而利用相似三角形的性质以及根据系数k的几何意义即可求得k的值．
解：设A（m，n），
∵S菱形ABCD=160，B（0，-5），
∴
（-2m）2（n+5）=160，
整理得-m（n+5）=80①，
作AF⊥x轴于F，
∴AF∥BD，
∴△AEF∽△BEO，
∴
,
∵E（-4，0），
∴
,
∴
,
把②代入①得，
,
解得m=-8，
∴n=5，
∴A（-8，5），
∵顶点A在反比例函数
的图象上,
∴k=-8×5=-40.
故选：C．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，如果每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球从发射出到第一次落在桌面的运行过程中，设乒乓球与端点A的水平距离为x（米），距桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：
t（秒） | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
x（米） | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
y（米） | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
（1）如果y是t的函数，
①如图，在平面直角坐标系tOy中，描出了上表中y与t各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；
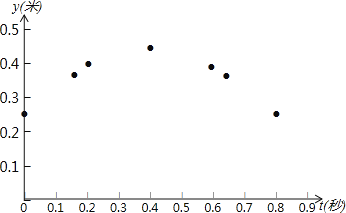
②当t为何值时，乒乓球达到最大高度？
（2）如果y是关于x的二次函数，那么乒乓球第一次落在桌面时，与端点A的水平距离是多少？
