题目内容
10.若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2012-a-b的值是( )| A. | 2020 | B. | 2018 | C. | 2017 | D. | 2016 |
分析 根据方程解的定义,求出a+b的值,即可解决问题.
解答 解:∵关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,
∴a+b+5=0,
∴a+b=-5,
∴2012-a-b=2012-(a+b)=2017.
故选C
点评 本题考查一元二次方程的解,解题的关键是理解方程的解的定义,属于基础题,中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列说法正确的是( )
| A. | 0.720精确到千分位 | B. | 3.6万精确到十分位 | ||
| C. | 5.0精确到个位 | D. | 3000精确到千位 |
15.一根蜡烛在凸透镜下成一实像,物距u,像距v和凸透镜的焦距f满足关系式$\frac{1}{u}$+$\frac{1}{v}$=$\frac{1}{f}$,f=6cm,v=8cm,则物距u的长为( )
| A. | 24cm | B. | 12cm | C. | $\frac{1}{24}$cm | D. | $\frac{1}{12}$cm |
2.下列两个变量之间的关系为反比例关系的是( )
| A. | 匀速行驶过程中,行驶路程与时间的关系 | |
| B. | 体积一定时,物体的质量与密度的关系 | |
| C. | 质量一定时,物体的体积与密度的关系 | |
| D. | 长方形的长一定时,它的周长与宽的关系 |
19.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法错误的是( )
| A. | 若c2=b2-a2,那么△ABC是直角三角形且∠C=90° | |
| B. | 若∠C-∠B=∠A,那么△ABC是直角三角形 | |
| C. | 若(c+a)(c-a)=b2,那么△ABC是直角三角形 | |
| D. | 若∠A:∠B:∠C=5:2:3,那么△ABC是直角三角形 |
 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点E从点B出发沿线段BA的方向移动到点A停止,连接CE.若△ADE与△CDE的面积相等,则线段DE的长度是$\frac{3\sqrt{13}}{5}$.
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点E从点B出发沿线段BA的方向移动到点A停止,连接CE.若△ADE与△CDE的面积相等,则线段DE的长度是$\frac{3\sqrt{13}}{5}$.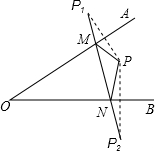 如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=22,则△PMN的周长为22.
如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=22,则△PMN的周长为22. 已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是x<-1或x>5.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是x<-1或x>5.