已知直角三角形的一个锐角为60度.斜边长为2.那么此直角三角形的周长是( )A．2.5B．3C．$\sqrt{3}$+2D．$\sqrt{3}$+3 题目和参考答案——青夏教育精英家教网—

题目内容

13．已知直角三角形的一个锐角为60度，斜边长为2，那么此直角三角形的周长是（　　）

A．

2.5

B．

C．

$\sqrt{3}$+2

D．

$\sqrt{3}$+3

分析根据直角三角形的性质：直角三角形中，30°所对的直角边是斜边的一半求得30°所对的直角边，然后利用勾股定理求得另一条直角边，即可解答．

解答解：解：如图所示，
Rt△ABC中，∠A=30°，AB=2，
故BC=$\frac{1}{2}$AB=$\frac{1}{2}$×2=1，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
故此三角形的周长是$\sqrt{3}$+3．
故选D．

点评本题考查了勾股定理和含30度角的直角三角形，熟悉直角三角形的性质：直角三角形中，30°所对的直角边是斜边的一半．熟练运用勾股定理是关键．

练习册系列答案

相关题目

3．一元二次方程3x²-2x-1=0的二次项系数和一次项系数分别为（　　）

4．

如图是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，m），且与x铀的一个交点在点（3，0）和（4，0）之间，则下列结论：
①abc＞0；②a-b+c＞0；③b²=4a（c-m）；④一元二次方程ax²+bx+c=m+1有两个不相等的实数根，其中正确结论的个数是（　　）

1．

如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点E从点B出发沿线段BA的方向移动到点A停止，连接CE．若△ADE与△CDE的面积相等，则线段DE的长度是$\frac{3\sqrt{13}}{5}$．

8．

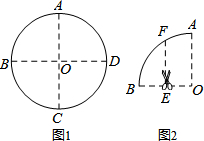如图1，将半径为2的圆形纸片沿圆的两条互相垂直的直径AC、BD两次折叠后，得到如图2所示的扇形OAB，然后再沿OB的中垂线EF将扇形OAB剪成左右两部分，则∠OEF=90°；右边部分经过两次展开并压平后所得的图形的周长为$\frac{4π}{3}$+4$\sqrt{3}$．

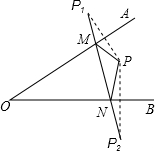18．$\frac{1}{\frac{1}{1339}+\frac{1}{1340}+…+\frac{1}{2007}}$的整数部分是2．

5．

如图：点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P₁，P₂，连接P₁P₂交OA于M，交OB于N，P₁P₂=22，则△PMN的周长为22．

2．下列两个变量之间的关系为反比例关系的是（　　）

	A．	匀速行驶过程中，行驶路程与时间的关系
	B．	体积一定时，物体的质量与密度的关系
	C．	质量一定时，物体的体积与密度的关系
	D．	长方形的长一定时，它的周长与宽的关系

3．下列函数中，y随x的增大而减小的函数是（　　）

试题分类