题目内容
 如图8,用同样规格黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题:
如图8,用同样规格黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题:
⑴ 在第n个图中,每一横行共有  块瓷砖,每一坚列共有 块瓷砖(均用含n的代数式表示);
块瓷砖,每一坚列共有 块瓷砖(均用含n的代数式表示);
⑵ 设铺设地面所用瓷砖的总块数为y,请写出y与(1)中的n的函数关系式(不要求写自变量n的取值范围);
⑶ 按上述铺设方案,铺一块这样的矩形地面共用了506块 瓷砖,求此时n的值;
瓷砖,求此时n的值;
⑷ 若黑瓷砖每块4元,白瓷砖每块3元,在问题⑶中,共需花多少元钱购买瓷砖?
⑸ 是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明为什么?
(1)n+3,n+2 (2)y=(n+3)(n+2),即y=n2+5n+6;(3)当y=506时,n2+5n+6=506
,解之得,n1=20,n2=-25(舍去);(4)白瓷砖块数是420块,黑瓷砖块数为86块,共需1604元;(5)n(n+1)= (n+3)(n+2)- n(n+1),化简为n2-3n-6=0,解得n1= , n1=
, n1= (舍去),因为n的值不为正整数,所以不存在黑、白瓷砖块数相等的情形。
(舍去),因为n的值不为正整数,所以不存在黑、白瓷砖块数相等的情形。

练习册系列答案
相关题目

 -2 = -2 (x )2 + ( );
-2 = -2 (x )2 + ( );
 (备用数据
(备用数据 ,
, 精确到1%)
精确到1%) 面墙为一边,再用13米的铁丝网围成一个面积为20平方米的长方形,求长方形的长和宽,设长为x米,根据题意可得方程( )
面墙为一边,再用13米的铁丝网围成一个面积为20平方米的长方形,求长方形的长和宽,设长为x米,根据题意可得方程( ) =20 C x (13-0.5x)=20 D
=20 C x (13-0.5x)=20 D  =20
=20 去浪淘尽,千古风流数人物;
去浪淘尽,千古风流数人物; 多少年华属周瑜?
多少年华属周瑜?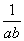 (B)
(B)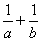 (C)
(C)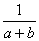 (D)
(D)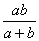
 (利息税为利息的20%),共取得10404元,求这种储蓄的年利率.(12分)
(利息税为利息的20%),共取得10404元,求这种储蓄的年利率.(12分)