题目内容
6.已知抛物线y=a(x-2)2+1的顶点为A,顶点为O,该抛物线交y轴正半轴于点B,且S△AOB=3(1)此抛物线所对应的函数关系式;
(2)x为何值时,y随x增大而减小?
分析 (1)根据三角形的面积求得B的坐标,代入解析式即可求得a,从而求得解析式;
(2)根据抛物线的性质即可求得.
解答 解:(1)由抛物线y=a(x-2)2+1可知顶点为A(2,1),
∵S△AOB=3,
∴$\frac{1}{2}$OB×2=3,
∴OB=3,
∴B(0,3)
把B(0,3)代入y=a(x-2)2+1得:3=a(0-2)2+1,解得a=$\frac{1}{2}$,
∴此抛物线所对应的函数关系式为y=$\frac{1}{2}$(x-2)2+1;
(2)当x<2时,y随x增大而减小.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数的性质,求得B的坐标是解题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | x4•x4=x16 | B. | a2+a2=a4 | C. | (a6)2÷(a4)3=1 | D. | (a+b)2=a2+b2 |
14.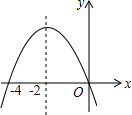 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
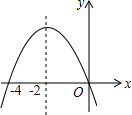 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )| A. | ①③④ | B. | ②④⑤ | C. | ①②⑤ | D. | ②③⑤ |
11.若关于x的不等式组$\left\{\begin{array}{l}x-m<0\\ 3-2x≤1\end{array}\right.$的所有整数解的和是10,则m的取值范围是( )
| A. | 4<m<5 | B. | 4<m≤5 | C. | 4≤m<5 | D. | 4≤m≤5 |
15.下列运算正确的是( )
| A. | 3a2•a3=3a6 | B. | 5x4-x2=4x2 | C. | (2a2)3•(-ab)=-8a7b | D. | 2x2÷2x2=0 |
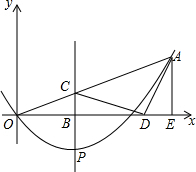 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.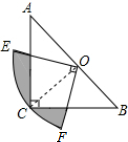 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.