题目内容
如图,一段抛物线 记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( )
记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( )

( ,
, )
)
【解析】
试题分析:根据旋转的性质,可得图形的大小形状没变,可得答案.
试题解析:y=-x(x-1)(0≤x≤1),
OA1=A1A2=1,P2P4=P1P3=2,
P2(1.5,-0.25)
P10的横坐标是1.5+2×[(10-2)÷2]=  ,
,
p10的纵坐标是- .
.
考点:二次函数图象与几何变换.

练习册系列答案
相关题目


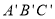 是位似图形,且△ABC与△
是位似图形,且△ABC与△
