题目内容
已知sinα=0.6,cosβ=0.8,试判断锐角α与β的关系 .
考点:锐角三角函数的增减性
专题:
分析:利用锐角三角函数关系的增减性得出45°>α>30°,45°<β<60°,进而得出答案.
解答:解:∵sinα=0.6,
∴sin30°<sinα<sin45°
∴45°>α>30°,
∵cosβ=0.8,
∴cos60°<cosβ<cos45°,
∴45°<β<60°,
故α<β.
故答案为:α<β.
∴sin30°<sinα<sin45°
∴45°>α>30°,
∵cosβ=0.8,
∴cos60°<cosβ<cos45°,
∴45°<β<60°,
故α<β.
故答案为:α<β.
点评:此题主要考查了锐角三角函数增减性,得出α、β的取值范围是解题关键.

练习册系列答案
相关题目
△ABC经过平移以后的图形为△EFG,那么下列说法正确的是( )
| A、△ABC≌△EFG |
| B、AE≠BF |
| C、AB不一定平行于EF |
| D、四边形ACGE不是平行四边形 |
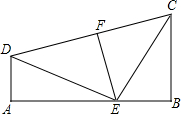 已知:如图,AD⊥AB于点A,BC⊥AB于点B.E是AB上一点,DE⊥CE,AE=BC.EF是△DEC的中线.求证:EF是CD的垂直平分线.
已知:如图,AD⊥AB于点A,BC⊥AB于点B.E是AB上一点,DE⊥CE,AE=BC.EF是△DEC的中线.求证:EF是CD的垂直平分线.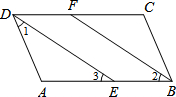 推理填空题.
推理填空题.